W tym zadaniu udowodnij, że dwusieczne wychodzące z kątów przy podstawie, trójkąta równoramiennego mają taką samą długość.
Rysunek pomocniczy:
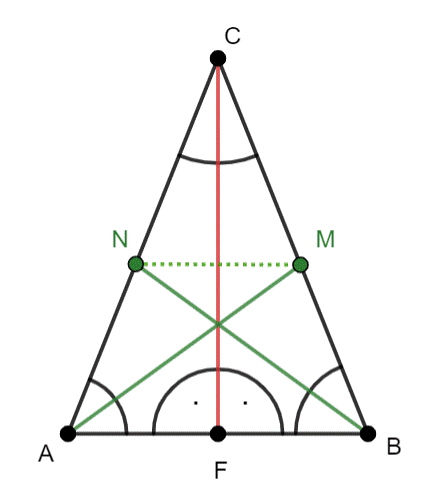
|AM|, |BN|–dwusieczne kątów |∡CAB| i |∡ABC|
Przyjmij:
|∡BAN| = |∡ABM| = α
|∡BAM| = |∡MAN| = |∡ABN| = |∡NBM| = 0.5α
Trójkąty ABE i ABM są przystające–cecha przystawania: (kąt–bok–kąt), więc:
|AM| = |BN|

W tym zadaniu skorzystaj z twierdzenia o dwusiecznej kąta, sumy kątów w trójkącie równoramiennym oraz z cech trójkątów przystających.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
