W tym zadaniu musisz obliczyć długości boków trójkąta prostokątnego, korzystając z założeń podanych w zadaniu.
R–promień okręgu opisanego na trójkącie prostokątnym
r–promień okręgu wpisanego na trójkącie prostokątnym
a, b–długości boków przyprostokątnych
c–długość boku przeciwprostokątnej
a + 17 = b
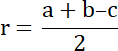
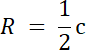
R + r = 15,5 cm
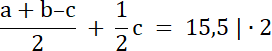
a + b–c + c = 31
a + b = 31
a + a + 17 = 31 |–17
2a = 14 |/2
a = 7 cm
b = a + 17 = 24 cm
a2 + b2 = c2
72 + 242 = c2
49 + 576 = c2
625 = c2 |/√
c = 25 cm
Długości boków trójkąta: 7 cm, 24 cm, 25 cm

W tym zadaniu skorzystaj ze wzoru na promień okręgu wpisanego oraz okręgu opisanego na trójkącie prostokątnym, a następnie z twierdzenia Pitagorasa, aby obliczyć długości odcinków trójkąta.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
