W tym zadaniu wyznacz promień okręgu, który został wpisany w trójkąt ABC, dla przykładu 3.
Rysunek pomocniczy:
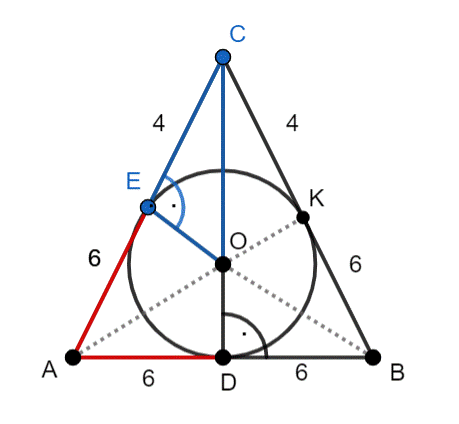
|OD| = |EO| = |OK| = r–promień okręgu wpisanego
|CD| = h–wysokość trójkąta równoramiennego
|CD|2 = 102–62
|CD|2 = 100–36 = 64 |/√
|CD| = 8
|AD| = |AE| = |DB| = |BK| = 6
|CE| = |AC|–|AE|
|CE| = 10–6 = 4
Trójkąty CEO i CDB są podobne–cecha podobieństwa: (kąt–kąt–kąt), więc:
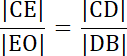
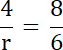
8r = 24 |/8
r = 3

W tym zadaniu wyznacz wysokość CD z twierdzenia Pitagorasa. Zauważ, że odcinki: |AD| = |AE| i |DB| = |BK|–z twierdzenia o odcinkach stycznych, a trójkąty CEO i CDB są podobne–cecha podobieństwa: (kąt–kąt–kąt), wiec skorzystaj ze stosunku podobieństwa trójkątów.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
