W tym zadaniu udowodnij, że jeśli kąty DOB = β i AOC = γ, to
![]()
Przyjmij:
P–punkt przecięcia cięciw AB i CD
Zauważ, że kąt środkowy |∡AOC| jest oparty nam tym samym łuku, co kąt wpisany |∡ABC| więc:
![]()
Dodatkowo kąt środkowy |∡DBC| jest oparty na takim samym łuku, co kąt wpisany |∡DCD|, więc:
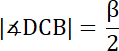
Trójkąt CBP:
|∡BPC| = 180°–0,5β–0,5γ
Zauważ, że kąty |∡BPC| i α są kątami przyległymi, więc:
|∡BPC| + α = 180°
180°–0,5β–0,5γ + α = 180° |–180°
α = 0,5β + 0,5γ
α = 0,5(β + γ)

W tym zadaniu skorzystaj własności kąta wpisanego opartego na tym samym łuku, a także z sumy miar kątów w trójkącie, żeby udowodnić tezę.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
