W tym zadaniu oblicz długość cięciwy okręgu o1, która jest styczna do okręgu o2.
Rysunek pomocniczy:
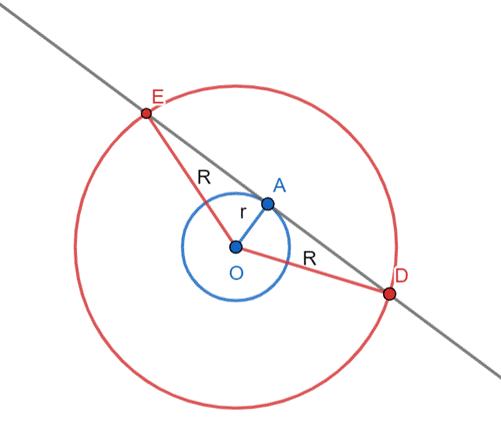
|ED|–cięciwa okręgu o1
|ED| = |EA| + |AD|
Trójkąt EOA:
|EO|2 = |EA|2 + |OA|2
R2 = |EA|2 + r2 |–r2
R2–r2 = |EA|2
9 = |EA|2 | /√
|EA| = 3
|ED| = |AD|
|ED| = 2|ED|
|ED| = 2∙3 = 6

W tym zadaniu skorzystaj z informacji o tym, że jeśli promień okręgu jest prostopadły do cięciwy, to dzieli ją na 2 równe odcinki i skorzystaj z twierdzenia Pitagorasa do wyznaczenia połowy odcinka cięciwy.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
