W tym zadaniu oblicz długość środkowej, która opada na podstawę |AB| w trójkącie ABC.
Zauważ, że trójkąt ABC jest prostokątny:
|AB|2 = |BC|2 + |AC|2
102 = 62 + 82
100 = 36 + 64
100 = 100
Rysunek pomocniczy:
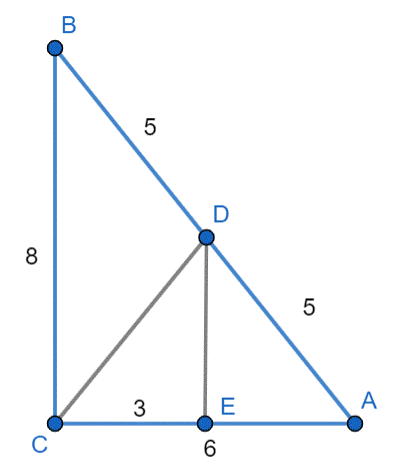
|DE| = 0,5∙|BC|
|DE| = 0,5∙8
|DE| = 4
Trójkąt CED jest prostokątny, więc:
|CD|2 = |CE|2 + |DE|2
|CD|2 = 32 + 42
|CD|2 = 9 + 16 = 25 |/√
|CD| = 5

W tym zadaniu skorzystaj z twierdzenia odwrotnego do twierdzenia Pitagorasa–udowodnisz, że trójkąt ABC jest prostokątny, następnie skorzystaj z twierdzenia o odcinku łączącym środki boków trójkąta.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
