W tym zadaniu musisz udowodnić, że wysokości w trójkącie równoramiennym, które wychodzą z wierzchołków podstawy tego trójkąta, są sobie równe.
Rysunek poglądowy:
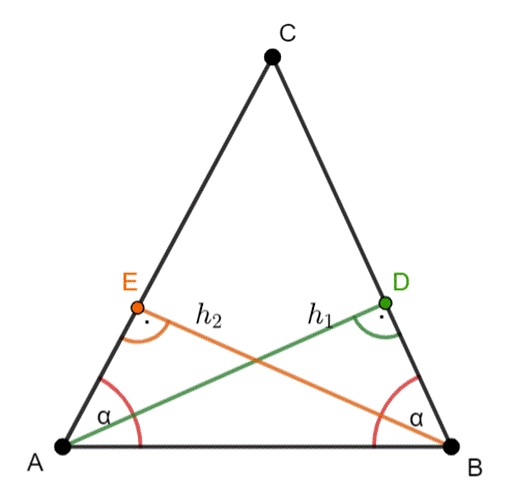
|AB|–podstawa trójkąta równoramiennego
|AC|, |BC|–ramiona trójkąta równoramiennego
|AC| = |BC|, więc: |∡CAB| = |∡ABC| = α
|AD| = h1–wysokość trójkąta
|BE| = h2–wysokość trójkąta
Skoro:
|∡BDA| = |∡BEA| = 90° i |∡CAB| = |∡ABC|, więc:
|∡ABE| = |∡ABD| = 90°–α
Skorzystaj z cechy przystawania trójkątów: kąt–bok–kąt–przy boku o tej samej długości, leżą kąty o tej samej mierze, więc w tym przypadku trójkąty: ABE i ABD są przystające, więc:
|AD| = |BE|, czyli h1 = h2

W tym zadaniu skorzystaj z definicji na wysokość trójkąta oraz cechy przystawania trójkątów (kąt–bok–kąt).

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
