W tym zadaniu oblicz promień okręgu opisanego na trójkącie prostokątnym.
Rysunek pomocniczy:
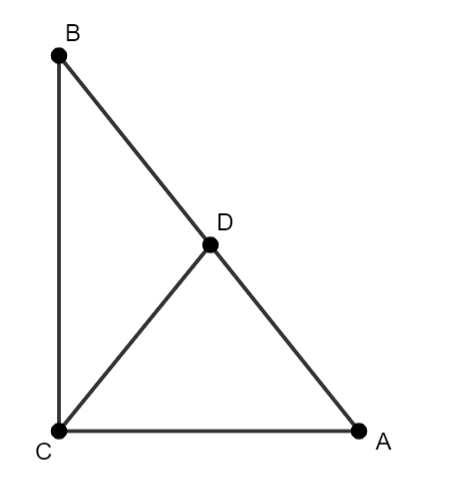
|CD|–wysokość opuszczona na podstawę
R–promień okręgu opisany na trójkącie
Trójkąt BCD–trójkąt prostokątny:
|BD|2 = |BC|2–|CD|2
|BD|2 = 122–(7,2)2
|BD|2 = 144–51,84
|BD|2 = 92,16 |/√
|BD| = 9,6 cm
Zauważ, że trójkąty BCD i ACD są podobne; cecha podobieństwa (kąt–kąt–kąt)
|∡BDC| = |∡ADC| = 90°, więc:
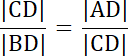
|CD|2 = |AD|∙|BD|
(7,2)2 = |AD|∙9,6
51,84 = |AD|∙9,6 |/9,6
|AD| = 5,4 cm
|AB| = |AD| + |BD|
|AB| = 5,4 + 9,6
|AB| = 15 cm
|AB| = 2R
2R = 15 |/2
R = 7,5 cm

W tym zadaniu skorzystaj ze wzoru na promień okręgu opisanym na trójkącie prostokątnym oraz z cechy podobieństwa trójkątów: kąt–kąt–kąt.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
