W tym zadaniu przepisz twierdzenie o odcinkach stycznych do zeszytu, a następnie narysuj okrąg oraz odcinki styczne do okręgu. Połącz punkty O i P, a na koniec udowodnij twierdzenie.
Rysunek poglądowy:
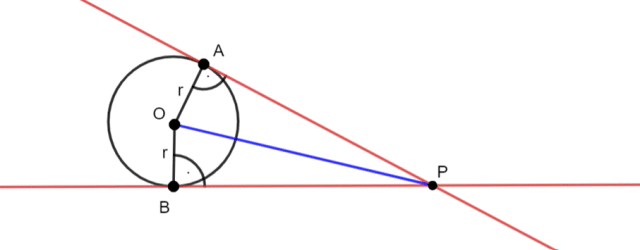
Założenia:
O–środek okręgu
r–promień okręgu: |OB| = |OA| = r
|PA|–styczna do okręgu w punkcie A
|PB|–styczna do okręgu w punkcie B
Teza:
|AP| = |PB|
Dowód:
Zauważ, że po połączeniu punktu O z P powstały dwa trójkąty prostokątne:
OBP i OPA, które mają 2 równe boki:
|OB| = |OA| i |OP| = |OP|
Skorzystaj z cechy trójkątów przystających: bok–kąt–bok i zauważ, że:
|AP| = |PB|

W tym zadaniu przerysuj rysunek, połącz punkty O i P. Następnie udowodnij tezę, korzystając z własności stycznych do okręgu oraz z cechy przystawania trójkątów (bok–kąt–bok).

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
