W tym zadaniu zapisz twierdzenie o środkowych w trójkącie. Dodatkowo określ, czy środek ciężkości trójkąta prostokątnego równoramienne znajduje się w tej samej odległości od wszystkich wierzchołków? Oblicz odległości dla przyprostokątnej trójkąta równej 3.
Środkowe w trójkącie to odcinki wychodzące z wierzchołków trójkąta, dzielące bok leżący naprzeciwko wierzchołka wychodzącego na dwa równe odcinki. Punkt przecięcia środkowych dzieli je na odcinki w stosunku 2:1, licząc od wierzchołka wychodzącego.
Rysunek pomocniczy:
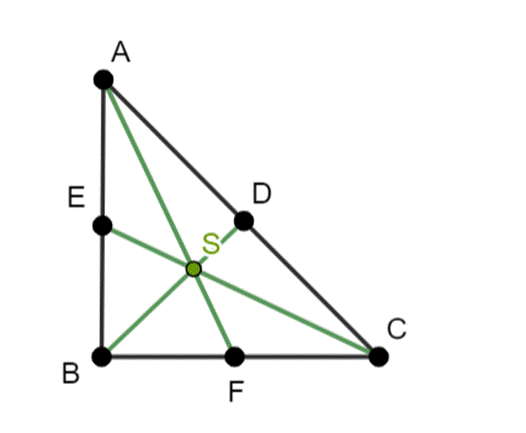
|AB| = |BC| = 3
|AF|, |BD|, |CE|–środkowe trójkąta
|AC| = 3√2
Środkowa przecina przeciwprostokątną pod kątem prostym i dzieli ją na dwa równe odcinki (własność trójkąta równoramiennego), więc:
|AD| = |DC| = 0,5∙3√2
Trójkąt BDC:
|BD|2 = |BC|2–|DC|2
|BD|2 = 32–(0,5∙3√2)2
|BD|2 = 9–4,5
|BD|2 = 4,5 |/√
|BD| = 0,5∙3√2
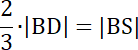
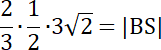
√2 = |BS|
Trójkąt ABD:
|AB|2 + |BF|2 = |AF|2
32 + (0,5∙3)2 = |AF|2
9 + 2,25 = |AF|2
11,25 = |AF|2 | /√
1,5∙√5 = |AF|
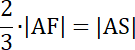
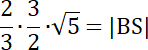
√5 = |BS|
|AS| ≠ |BS
Środek ciężkości nie znajduje się w jednakowej odległości od wierzchołków trójkąta prostokątnego równoramiennego.

W tym zadaniu skorzystaj z twierdzenia o środkowych w trójkącie oraz z twierdzenia Pitagorasa.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
