W tym zagadaniu wykonaj konstrukcję trójkąta prostokątnego, którego najdłuższa przekątna jest równa √15.
Zwróć uwagę, że:
12 + (√15)2 = 42
Skonstruuj trójkąt prostokątny, który ma:
Przyprostokątne długości: 1, √15,
Przeciwprostokątna równa 4
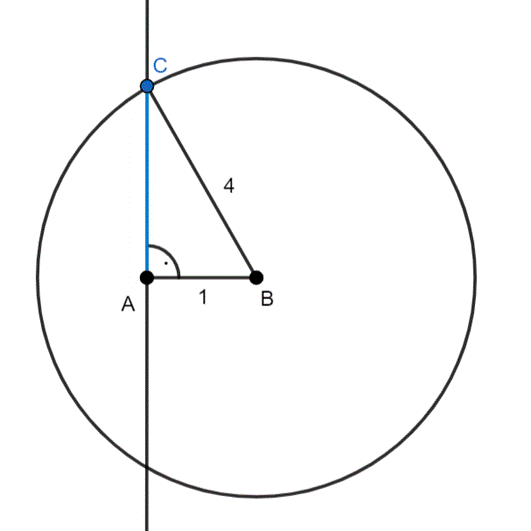

W tym zadaniu najpierw zauważ, że odcinek równy √15 to przyprostokątna trójkąta prostokątnego, gdzie 4–długość przeciwprostokątnej, a 1 to długość drugiej przyprostokątnej–z twierdzenia Pitagorasa.
Konstrukcja odcinka długości √15:
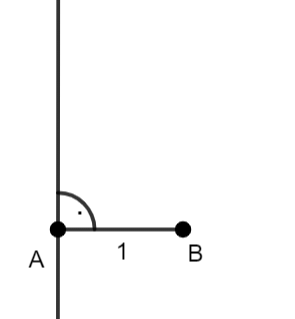
–narysuj odcinek |AB o długości 1
–poprowadź prostą prostopadła do odcinka |AB|, która przechodzi przez punkt A
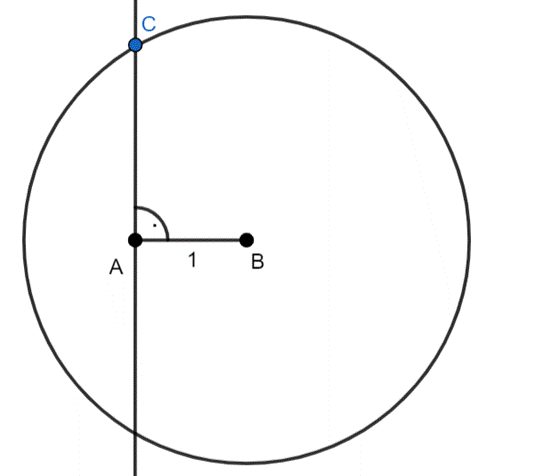
–następnie narysuj okrąg o promieniu 4, a środek okręgu znajduje się w punkcie B
–na koniec połącz punkt B i C, dzięki czemu powstał trójkąt prostokątny, gdzie |AC| = √15

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
