W tym zadaniu wyznacz miarę kąta α.
Rysunek pomocniczy:
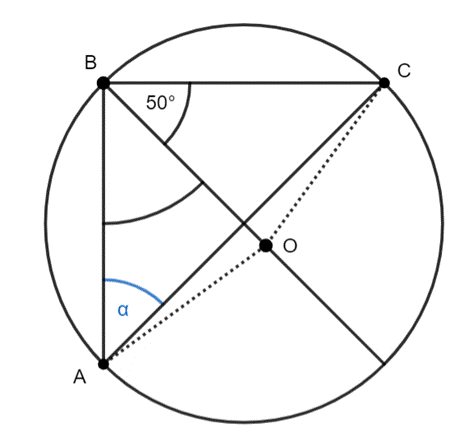
r–promień okręgu
|BO| = |CO| = r
Trójkąt BOC–trójkąt równoramienny
|∡OBC| = |∡BCO| = 50°
|∡BOC| = 180°–|∡OBC|–|∡BCO|
|∡BOC| = 180°–50°–50°
|∡BOC| = 80°
|∡BAC| = 0,5∙|∡BOC|
|∡BAC| = 0,5∙80° = 40°
Odpowiedź A. 40°

W tym zadaniu skorzystaj z twierdzenia na kąt wpisany i środkowy, które oparte są na tym samym łuku.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
