W tym zadaniu na podstawie długości promienia wpisanego w trójkąt prostokątny, oblicz długość przyprostokątnej tego trójkąta.
Rysunek pomocniczy:
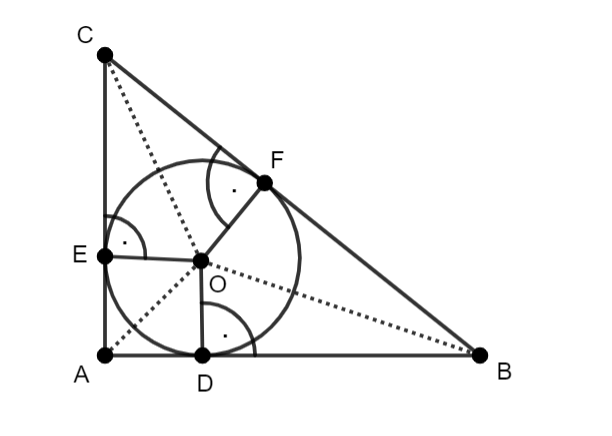
Przyjmij:
|AC| = |AB| = a–przyprostokątne trójkąta
|BC| = b–przeciwprostokątna trójkąta
r–promień okręgu wpisanego w trójkąt
|AB|2 + |AC|2 = |BC|2
a2 + a2 = b2
2a2 = b2 | /√
b = a√2
|AE| = |AD| = r
|CE| = |CF| = a–r
|CF| = a–(2–√2) = a–2 + √2
|DB| = |BF| = a–(2–√2) = a–2 + √2
|BC| = a√2
|CF| + |BF| = a√2
a–2 + √2 + a–2 + √2 = a√2
2a–4 + 2√2 = a√2 |–2a
–4 + 2√2 = a√2–2a
–4 + 2√2 = a(√2–2) | (√2–2)
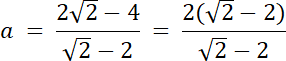
a = 2

W tym zadaniu skorzystaj z twierdzenia o odcinkach stycznych.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
