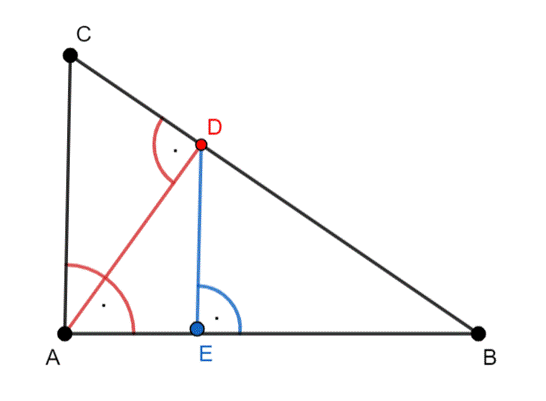
W tym zadaniu, na podstawie informacji o trójkącie ABC, oblicz wysokość DE w trójkącie ABD.
Rysunek pomocniczy:
![]()
![]()
|AD| = 2
Trójkąt ADC:
|AD|2 + |CD|2 = |AC|2
22 + 12 = |AC|2
4 + 1 = |AC|2
5 = |AC|2 | /√
|AC| = √5
Trójkąty: ABC i EBD są podobne–cecha podobieństwa: kąt–kąt–kąt
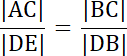
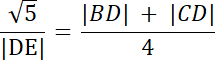
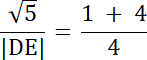
5|DE| = 4√5 | /5
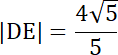

W tym zadaniu skorzystaj ze wzoru na wysokość trójkąta prostokątnego poprowadzoną z wierzchołka kąta prostego oraz z twierdzenia Pitagorasa, a także wykorzystaj cechę podobieństwa trójkątów: kąt–kąt–kąt.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
