W tym zadaniu musisz udowodnić, że środkowa, poprowadzona na podstawę trójkąta równoramiennego jest jego wysokością.
Rysunek poglądowy:
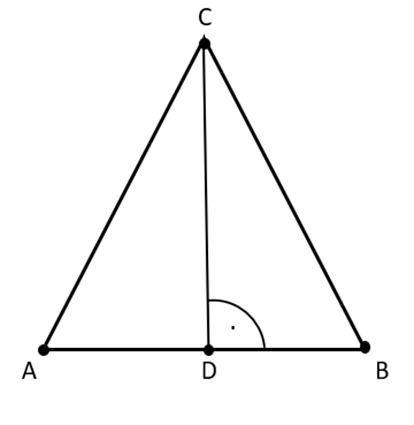
Trójkąt ABC–trójkąt równoramienny, gdzie
AC i BC–ramiona trójkąta
|AC| = |BC|⇒ |∡CAB| = |∡ABC|,
Przyjmij, że: |∡CAB| = |∡ABC| = α
|∡BCA| = 180°–(|∡CAB| + |∡ABC|)
|∡BCA| = 180°–(α + α)
|∡BCA| = 180°–2α
Środkowa trójkąta: |CD|, więc:
|AD| = |DB|
Trójkąty ADC i CDB mają boki tej samej długości: trójkąty są przystające–cecha przystawania: bok–bok–bok, więc |∡ADC| = |∡CDB|.
Skoro kąty są równe, to bok |CD| jest nachylony do boku |AB| pod kątem prosty–czyli jest wysokością opuszczoną na ten bok.

W tym zadaniu skorzystaj z definicji na wysokość trójkąta, środkową trójkąta oraz cechy przystawania trójkątów (bok–bok–bok).

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
