W tym zadaniu udowodnij powyższą tezę o dwusiecznej kąta przy podstawie trójkąta.
|BD|–dwusieczna kąta |∡ABC|
Przyjmij:
|∡CBD| = |∡DBA| = α
Rysunek pomocniczy:
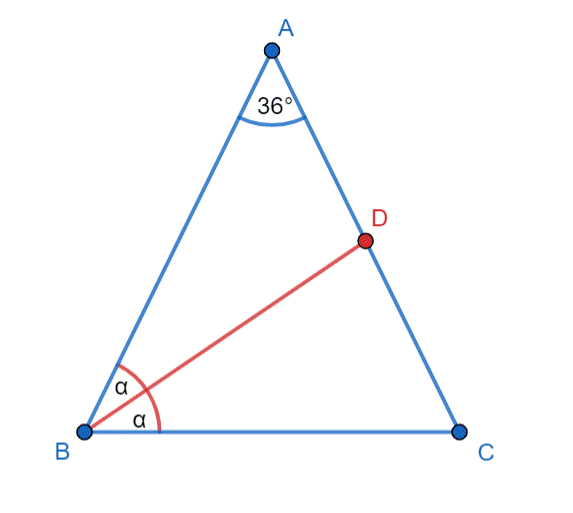
Trójkąt ABC–równoramienny i |AB| = |AC|, więc:
|∡ABC| = |∡BCA|
|∡ABC| = 2α
|∡BCA| = 2α
Suma miar kątów trójkąta:
|∡ABC| + |∡BCA| + |∡BAC| = 180°
2α + 2α + 36° = 180° |–36°
4α = 144° | /4
α = 36°
|∡ABD| = 36°, więc
Trójkąt ABD jest równoramienny–ma dwa kąty o takiej samej mierze
Trójkąt DBC–kąty:
|∡DBC| = α = 36°
|∡BCD| = 2α = 2∙36° = 72°
|∡CDB| = 180°–|∡BCD|–|∡DBC|
|∡CDB| = 180°–72°–36°
|∡CDB| = 72°, więc:
|∡CDB| = |∡BCD|, więc trójkąt DBC jest równoramienny

W tym zadaniu skorzystaj z definicji dwusiecznych oraz sumy kątów wewnętrznych w trójkącie. Dodatkowo skorzystaj z własności trójkąta równoramiennego.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
