W tym zadaniu narysuj za pomocą cyrkla i linijki skonstruuj trójkąt prostokątny równoramienny, którego przeciwprostokątna jest długości a.
x–długość boku przyprostokątnej,
zauważ: |AB| = |AC|–trójkąt równoramienny, więc:
|AB| = |AC| = |BC|2
x2 + x2 = a2
2x2 = a2 |/2
x2 = 0.5a2 |/√
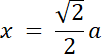
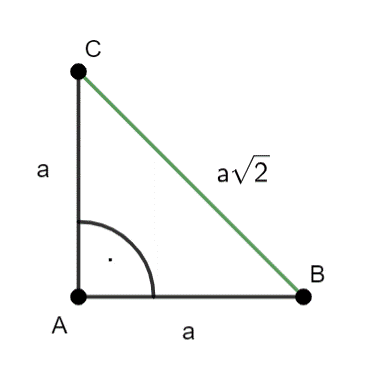
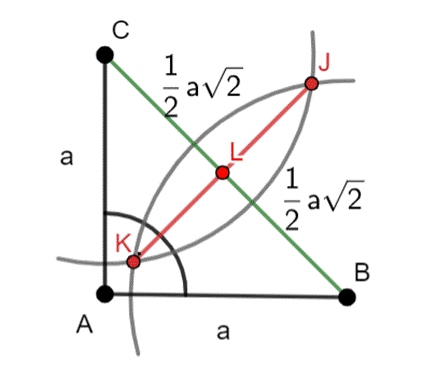
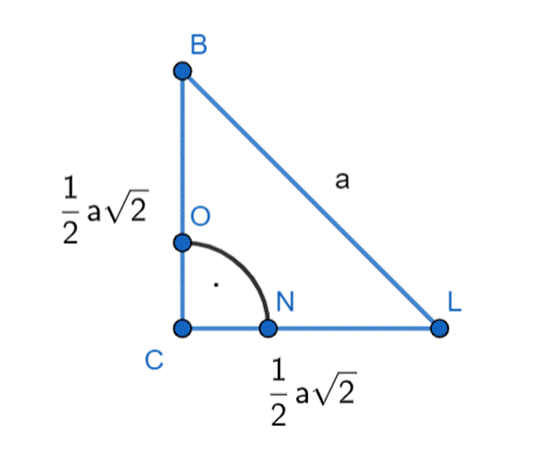

W tym zadaniu najpierw wyznacz długość przeciwprostokątnej trójkąta, skorzystaj z twierdzenia Pitagorasa. Następnie narysuj prostopadłe odcinki |AB| i |AC|, gdzie |AB| = |AC|. Połącz punkty B i C, dzięki czemu otrzymasz odcinek |BC| = a√2. Następnie skonstruuj symetralną odcinka |BC|, a powstały odcinek |CL| i |BC| to przyprostokątna trójkąta o przeciwprostokątnej równej a. Przenieś odcinek, narysuj do niego prostopadły odcinek, a skrajne punkty połącz.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
