W tym zadaniu oblicz obwód trójkąta ABC.
Wyprowadź odcinek CD w trójkącie–wysokość poprowadzoną z wierzchołka C:
Rysunek pomocniczy:
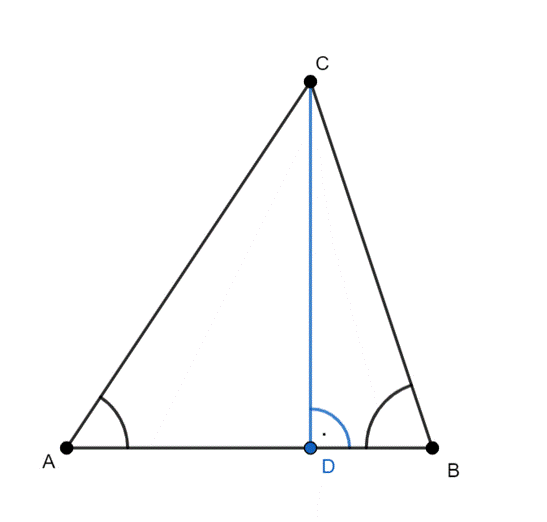
W trójkącie ADC:
|∡BAC| = 45°, |∡ADC| = 90°, więc |∡DCA| = 180°–45°–90° = 45°
Trójkąt jest równoramienny, więc:
|AD| = |CD| oraz |AC|2 = |AD|2 + |CD|2
|AC|2 = 2|AD|2
(3√2)2 = 2|AD|2
18 = 2|AD|2 | /2
9 = |AD|2 |√
3 = |AD|
|AD| = |CD| = 3
Trójkąt CDB:
|∡CBD| = |∡CBA| = 60°, |∡CDB| = 90°, więc |∡BCD| = 180°–60°–90° = 30°
Zauważ, że trójkąt ten jest połową trójkąta równobocznego, w którym zachodzi następująca zależność:
2|DB| = |BC|
|CD| = |DB|∙√3
3 = |DB|√3 / √3
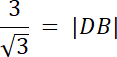
√3 = |DB|
|BC| = 2∙√3 = 2√3
Obwód trójkąta ABC:
LABC = |AB| + |BC| + |AC|
LABC = (|AD| + |DB|) + |BC| + |AC|
LABC = (3 + √3) + 2√3 + 3√2
LABC = 3√3 + 3√2 + 3
LABC = 3(1 + √2 + √3)

W tym zadaniu wyprowadź wysokość CD na podstawę AB, dzięki czemu otrzymasz dwa trójkąty prostokątne, a z twierdzenia Pitagorasa wyznacz długości boków. Skorzystaj również z własności miar kątów w trójkącie równobocznym.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
