W tym zadaniu na podstawie długości boków określ rodzaj trójkąta, a następnie oblicz odległość między środkiem okręgu a środkiem ciężkości tego trójkąta.
52 + 52 = 25 + 25 = 50
82 = 64
52 + 52 < 82
Podany trójkąt jest trójkątem rozwartokątnym.
Rysunek pomocniczy:
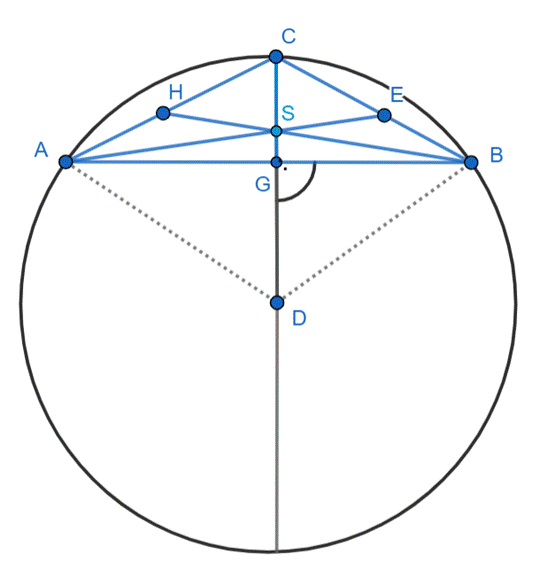
D–środek okręgu
S–środek ciężkości
|SD|–odległość środka okręgu od punktu ciężkości
|CD|–promień okręgu
|BH|, |AE|, |CG|–środkowe
|CG|–wysokość trójkąta
|AC| = |BC| = 5 cm
|AB| = 8 cm
|AG| = |GB| = 4 cm
|AH| = |CH| = |CE| = |EB| = 2,5 cm
|AC|2 = |CG|2 + |AG|2
52 = |CG|2 + 42
25 = |CG|2 + 16 |–16
|CG|2 = 9|/√
|CG| = 3
Odcinek |CS|
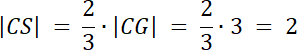
PABC = 0,5∙|CG|∙|AB|
PABC = 0,5∙3∙8
PABC = 12
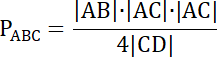
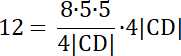
48|CD| = 200 |/48
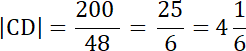
|SD| = |CD|–|CS|
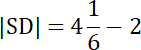
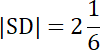

W tym zadaniu najpierw skorzystaj z nierówności kwadratowej, aby określić, czy trójkąt jest ostrokątny, prostokątny czy rozwartokątny. Następnie skorzystaj z zależności środkowej trójkąta oraz środka ciężkości. Zauważ, gdzie znajduje się środek okręgu, a gdzie środek ciężkości trójkąta. Wyznacz odległość między tymi punktami, korzystając z dwóch wzorów na pole trójkąta i odejmij odcinek |CS| od długości promienia.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
