W tym zadaniu musisz udowodnić, że proste BK i BL są styczne do okręgu o1. Sprawdź również, czy proste AK i AL są styczne do okręgu o2.
Rysunek pomocniczy:
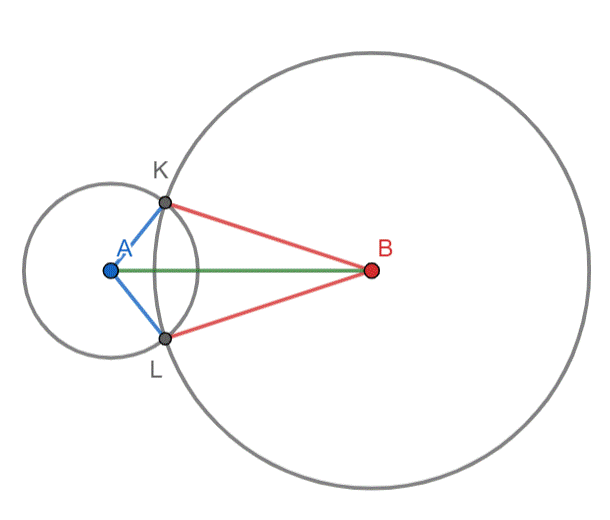
|AK| = |AL| = 8
|BK| = |BL| = 15
|AB| = 17
Zauważ, że trójkąty AKB i ALB są prostokątne:
|AK|2 + |BK|2 = |AB|2
82 + 152 = 172
64 + 225 = 289
289 = 289
kąty |∡AKB| i |∡ALB| to kąty proste, więc proste BK i BL są styczne do okręgu o1
proste AK i AL są styczne do okręgu o2.

W tym zadaniu skorzystaj z twierdzenia o stycznej do okręgu i twierdzenia odwrotnego do twierdzenia Pitagorasa, żeby udowodnić tezę.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
