W tym zadaniu określ, czy kąt BAC jest kątem prostym.
Rysunek pomocniczy:
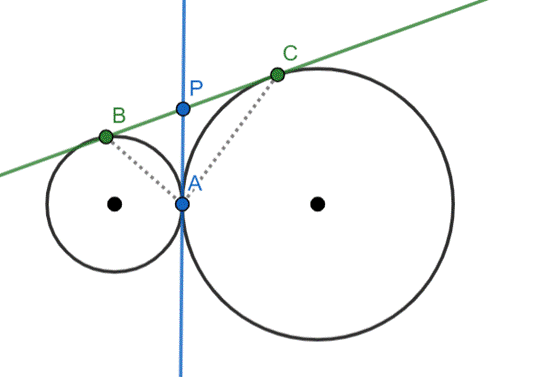
|BP| = |PA|, więc trójkąt BPA–trójkąt równoramienny
|∡ABP| = |∡BAP| = α
|∡BPA| = 180°–2α
|AP| = |PC|, więc trójkąt APC–trójkąt równoramienny
|∡ACP| = |∡PAC| = β
|∡APC| = 180°–2β
|∡BPA| + |∡APC| = 180°
180°–2α + 180°–2β = 180°
90°–α–β = 0
α + β = 90°
|∡BAC| = |∡BAP| + |∡PAC|
|∡BAC| = α + β = 90°

W tym zadaniu skorzystaj z twierdzenia o odcinkach stycznych, a także wykorzystaj informacje o sumie miar kątów w trójkącie. Dodatkowo wykorzystaj informację o kątach leżących na jednej prostej.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
