W tym zadaniu musisz obliczyć długości odcinków, na jakie został podzielony trójkąt, przez punkty styczności.
c–długość przeciwprostokątnej
a, b–długości przyprostokątnych
r–promień okręgu wpisanego w trójkąt prostokątny
Informacje, z podpunktu a:
c = 15 cm i r = 3 cm
Rysunek pomocniczy:
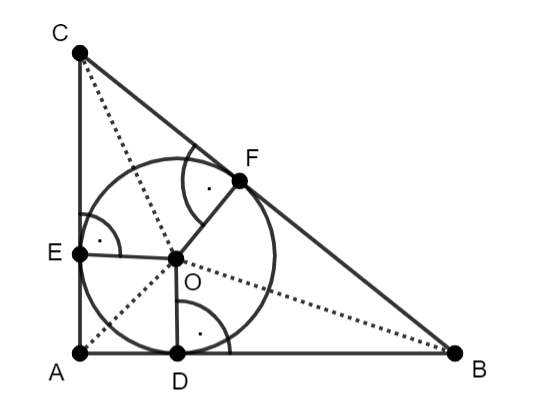
Przyjmij:
|AB| = 12, |AC| = 9, |BC| = 15
|OD| = |OE| = |OF| = r–promień okręgu wpisanego
|CE| = |CF|
|EO| = |OD|
|DB| = |BF|
Czworokąt EODA to kwadrat, więc:
|AD| = |DO| = |EO| = |AE| = r, więc:
|BC| = |CF| + |BF|
|CE| = |CF| = 9–r = 9–3 = 6 cm
|DB| = |BF| = 12–r = 12–3 = 9 cm
Przyprostokątna podzielona jest na odcinki o długości: 6 cm i 9 cm

W tym zadaniu wyznacz długości odcinków, na jakie została podzielona przeciwprostokątna przez punkt styczności–wykorzystaj twierdzenie o odcinkach stycznych.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
