W tym zadaniu określ na podstawie długości boków, jaki to trójkąt oraz oblicz promień okręgu, który jest opisany na tym trójkącie.
172 + 172 = 289 + 289 = 578
302 = 900
172 + 172 < 302
Trójkąt jest równoramienny rozwartokątny
Rysunek pomocniczy:
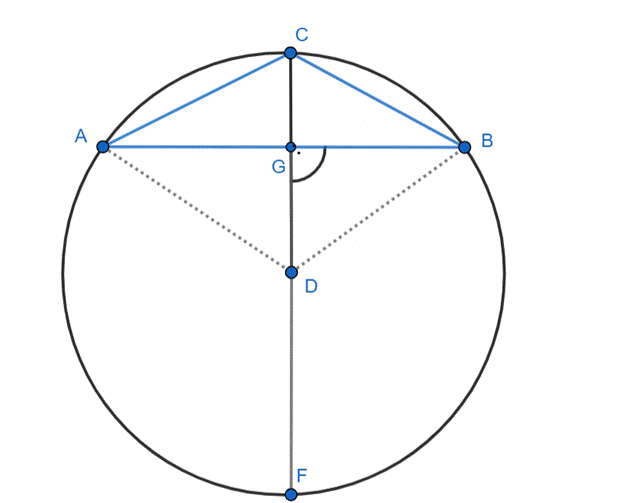
|AD| = |DB| = |CG| = |DF| = R–promień okręgu
|CG|–wysokość trójkąta
|AB| = |AG| + |GB|
|AG| = |GB|
|AB| = 2|GB|
30 = 2|GB| |/2
15 = |GB|
Trójkąt CGB:
|CG|2 = |BC|2–|BG|2
|CF|2 = 172–152
|CF|2 = 289–225
|CF|2 = 64 |/√
|CF| = 8
Przyjmij, że:
|GD| = 8 + r
Trójkąt GDB:
|BD|2 = |DG|2 + |BG|2
R2 = 152 + (8–R)2
R2 = 225 + 64–16R + R2 |–R2 + 16R
16R = 289 | /16
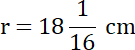

W tym zadaniu najpierw sprawdź, wykorzystując nierówność trójkątów, aby dowiedzieć się, czy trójkąt jest ostrokątny, czy rozwartokątny, a następnie skorzystaj własności promienia okręgu opisanego na trójkącie równoramiennym. Na koniec skorzystaj z twierdzenia Pitagorasa, żeby wyznaczyć długość promienia okręgu.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
