W tym zadaniu należy obliczyć długość odcinka AS oraz wyznaczyć długość środkowej AE.
Rysunek poglądowy:
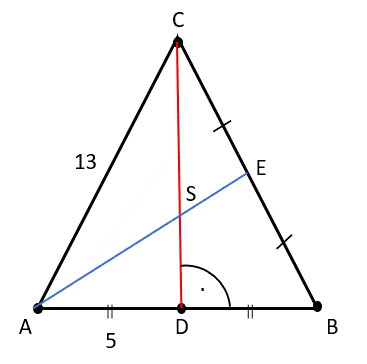
|AC| = |BC|–trójkąt równoramienny
|CD|–środkowa i wysokość trójkąta ABC
|CD| = 12–dane z przykładu 3. strona 110
|CD| = |CS| + |SD|
Przyjmij, że |SD| = x
|SD| : |CS| = 1:2
|CS| = 2|SD|
|CD| = 2|SD| + |SD|
12 = 3|SD| / 3
|SD| = 4
Zauważ, że trójkąt ADS jest prostokątny, a |AS| to przeciwprostokątna w tym trójkącie, więc:
|AS|2 = |AD|2 + |SD|2
|AS|2 = 52 + 42
|AS|2 = 25 + 16
|AS|2 = 41 | /√
|AS| = √41
|AE| = |AS| + |SE|
|SE| : |AS| = 1 : 2
2|SE| = |AS|
2|SE| = √41 / 2
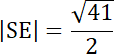
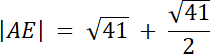
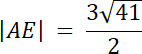

W tym zadaniu skorzystaj z twierdzenia o środkowych w trójkącie i wykorzystaj twierdzenie odwrotne do twierdzenia Pitagorasa, aby wyznaczyć długość odcinka |AS|.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
