W tym zadaniu oblicz miary kątów w trójkątach ACB oraz BCD.
Rysunek pomocniczy:
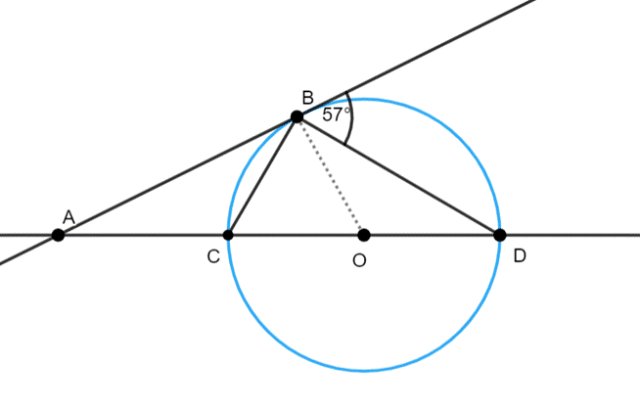
|∡B|–kąt dopisany oparty, na łuku BD
|∡B| = 57°,
|∡BCD|–oparty jest również, na łuku BD, więc:
|∡BCD| = |∡B| = 57°
Trójkąt BCD:
|∡DBC| = 90°–kąt wpisany, oparty na półokręgu
|∡CDB| = 180°–|∡BCD|–|∡DBC|
|∡CDB| = 180°–57°–90°
|∡CDB| = 33°
Trójkąt ACB:
|∡CBA| = 180°–|∡DBC |–57°
|∡CBA| = 180°–90°–57°
|∡CBA| = 33°
|∡ACB| = 180°–|∡BCD|
|∡ACB| = 180°–57°
|∡ACB| = 123°
|∡ACB| = 180°–|∡ACB|–|∡CBA|
|∡ACB| = 180°–123°–33°
|∡ACB| = 24°

W tym zadaniu skorzystaj z twierdzeń o kątach wpisanym i dopisanym oraz kątach wpisanym i środkowym, opartych na tym samym łuku. Przy obliczeniach skorzystaj z własności kątów w trójkącie oraz wartości kątów opartych na jednej prostej.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
