W tym zadaniu oblicz promień okręgu, który jest opisany na trójkącie prostokątnym.
R–promień okręgu opisanego
c–przeciwprostokątna trójkąta równoramiennego
a, b–przyprostokątne trójkąta prostokątnego, gdzie:
a = 15 cm i b = 20 cm
a2 + b2 = c2
152 + 202 = c2
225 + 400 = c2
625 = c2 |√
25 = c
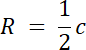
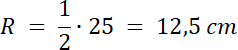

W tym zadaniu skorzystaj z twierdzenia Pitagorasa na wyznaczenie długości przeciwprostokątnej oraz z zależności długości promienia okręgu opisanego na trójkącie prostokątnym.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
