W tym zadaniu określ, jakimi cechami charakteryzuje się trójkąt, którego wierzchołki to punkty A i B, oraz jeden z punktów wspólny z okręgami o środkach A, B.
Rysunek poglądowy:
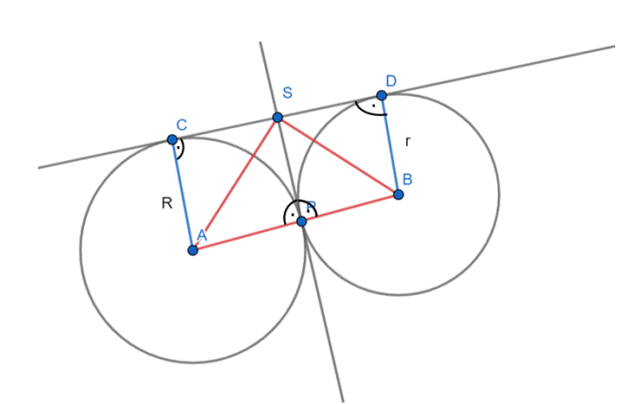
|CS| = |SD|
|CS| = |SP|, |SP| = |SD|
Trójkąty ACS i APS są przystające, cecha bok – bok – bok, więc:
|∡ASC| = |∡ASP| = α
|∡CAS| = |∡SAP| = 90°–α
Trójkąty PBS i BDS są przystające, cecha bok – bok – bok, więc:
|∡BSP| = |∡DSB| = β
|∡SBP| = |∡DBS| = 90°–β
|∡DSC| = 180°
|∡ASC| + |∡PSA| + |∡BSP| + |∡DSB| = 180°
α + α + β + β = 180°
α + β = 90°
|∡PSA| + |∡BSP| = 90°
|∡ASB| = 90°

W tym zadaniu skorzystaj z twierdzenia o odcinkach stycznych oraz wykorzystaj informacje o sumie miar kątów w trójkącie.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
