W tym zadaniu sprawdź, czy w trójkącie ABC z przykładu 1., kąt CSB może mieć miarę 90°.
Rysunek pomocniczy:
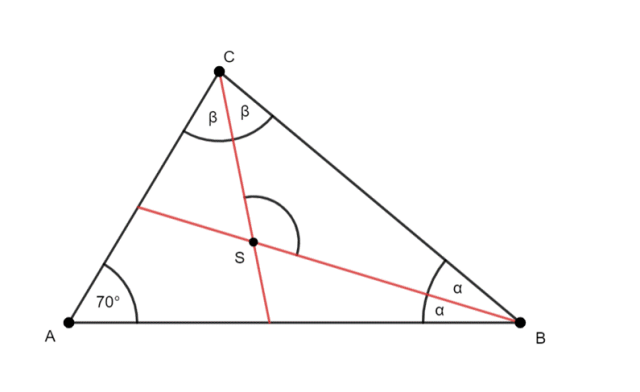
Z rysunku:
2α + 2β + 70° = 180° |–70°
2α + 2β = 110°
2(α + β) = 110° |/2
α + β = 65°
Trójkąt CSB:
α + β + |∡CSB| = 180°
65° + |∡CSB| = 180° |–65°
|∡CSB| = 115°
|∡CSB| ≠ 90°–kąt CSB, nie może być kątem prostym.

W tym zadaniu skorzystaj z twierdzenia o dwusiecznej kąta i znajomości sumy kątów w trójkącie.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
