W tym zadaniu narysuj odcinek o długości: √a2 + b2.
x–szukana długość odcinka
√a2 + b2 = x |2
a2 + b2 = x2
Zauważ:
a2 + b2 = x2
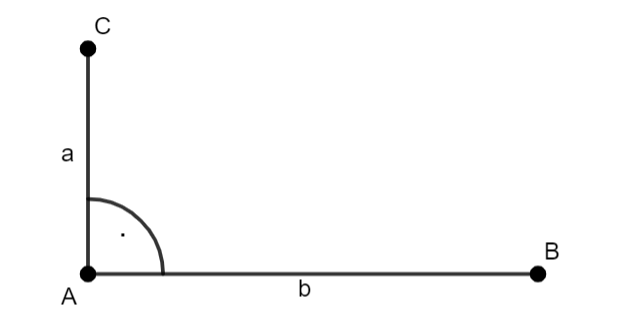

W tym zadaniu zauważ, że długość odcinka wyznaczysz z twierdzenia Pitagorasa na długość przeciwprostokątną trójkąta prostokątnego.
Konstrukcja:
–w pierwszym kroku narysuj dwa odcinki o długości: a i b, które są prostopadłe do siebie. Punkt przecięcia prostych oznacz literką A
–na prostej |AB| nałóż odcinek o długości a, którego początek jest w punkcie A, a koniec odcinka zaznacz jako b
–na prostej |AC| odłóż odcinek o długości b, którego początek będzie punkt A, a koniec odcinka zaznacz literką C
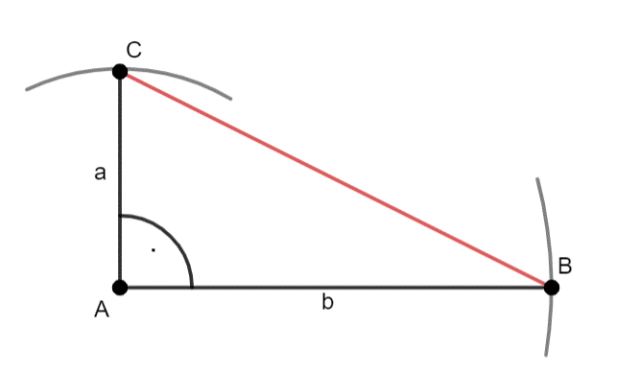
–zarysuj odcinek łączący punkt B i C. Jest to odcinek od długości: √a2 + b2.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
