W tym zadaniu, na podstawie stosunku długości łuków, wyznacz miary kątów w trójkącie ABC.
Rysunek poglądowy:
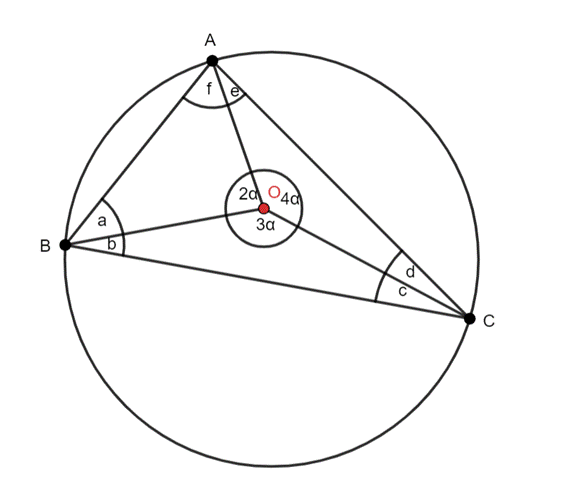
2α + 3α + 4α = 360°
9α = 360° |/9
α = 40°
|∡B| = a + b
4α = 2∙(a + b) | /2
2α = a + b
2∙40° = a + b
80° = a + b
|∡B| = 80°
|∡C| = c + d
2α = 2∙(c + d) | /2
α = c + d
40° = c + d
|∡C| = 40°
|∡A| = e + f
3α = 2∙(e + f) | /2
1,5∙α = e + f
1,5∙40° = e + f
60° = e + f
|∡A| = 60°
Kąty trójkąta ABC: 40°, 60°, 80°

W tym zadaniu wykorzystaj informację, że okrąg ma miarę wewnętrzną równą 360° i skorzystaj z twierdzenia o kątach wpisanym i środkowym, opartych na tym samym łuku.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
