W tym zadaniu udowodnij twierdzenie o cięciwach. Wykorzystaj do tego cechę podobieństwa trójkątów APC i BPD.
Rysunek pomocniczy:
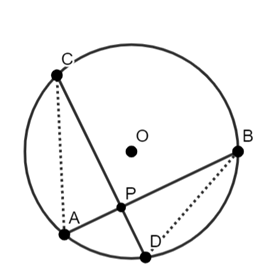
|∡ACD| = |∡ABD|–kąty wpisane, oparte na tym samym łuku,
|∡CAB| = |∡BDC|–kąty wpisane, oparte na tym samym łuku,
Dodatkowo:
|∡CPA| = |∡DPB|–kąty wierzchołkowe, więc trójkąty APC i BPD są podobne, cecha podobieństwa: kąt–kąt–kąt.
Daje nam to zależność:
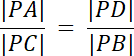
|PA|∙|PB| = |PC|∙|PD|

W tym zadaniu skorzystaj z twierdzenia o kątach wpisanych, opartych na tym samym łuku i z cechy podobieństwa trójkątów: (kąt–kąt–kąt).

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
