W tym zadaniu sprawdź, czy dwusieczna kąta AOC jest zawarta w dwusiecznej BD⇒.
Rysunek pomocniczy:
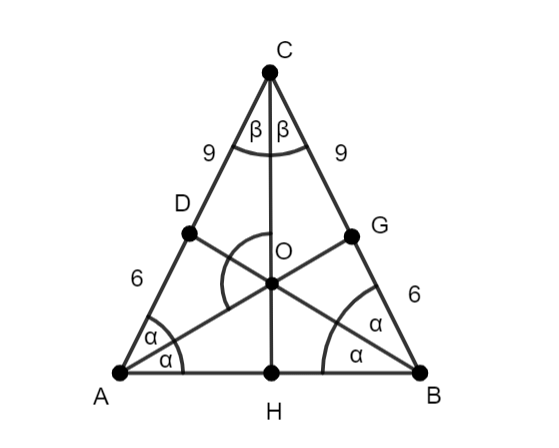
Skoro
|AC| = |BC| to dwusieczna kąta |∡CAB| i |∡ABC| dzieli odcinki ramion na odcinki: 9 i 6.
Trójkąt ABC
4α + 2β = 180° |/2
2α + β = 90°
Trójkąt AOH:
|∡OAH| = α
|∡AHO| = 90°, bo |CH| to wysokość w trójkącie równoramiennym ABC
|∡AOH| = 180°–90°–α
|∡AOH| = 90°–α
|∡AOH| = 2α + β–α = α + β
Trójkąt ABO–równoramienny–kąty przy podstawie mają równą wartość, więc:
|∡AOH| = |∡BOH|
Kąty wierzchołkowe, mają taką samą miarę, więc:
|∡AOH| = |∡COG| = α + β
|∡BOH| = |∡COD| = α + β
|∡AOD| = |∡BOF|
Suma miar kąta pełnego = 360°
|∡AOD| + |∡BOF| + |∡AOH| + |∡COG| + |∡BOH| + |∡COD| = 360°
2|∡AOD| + 2(α + β) = 360° |/2
|∡AOD| + α + β = 180°
|∡AOD| + α + β = 4α + 2β |–(α + β)
|∡AOD | = 3α + β
Więc:
|∡AOD | = |∡COD|
3α + β = α + β–równanie sprzeczne
α > 0 i β > 0
Dwusieczna kąta |∡AOC| nie zawiera się w dwusiecznej BD⇒.

W tym zadaniu skorzystaj z twierdzenia o sumie kątów w trójkącie, wartości kąta pełnego oraz zależności kątów wierzchołkowych. Przy rozwiązywaniu pamiętaj, że dwusieczna dzieli kąt na katy o dwóch równych miarach.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
