W tym zadaniu oblicz promień okręgu wpisanego w trójkąt dwoma sposobami.
Rysunek pomocniczy:
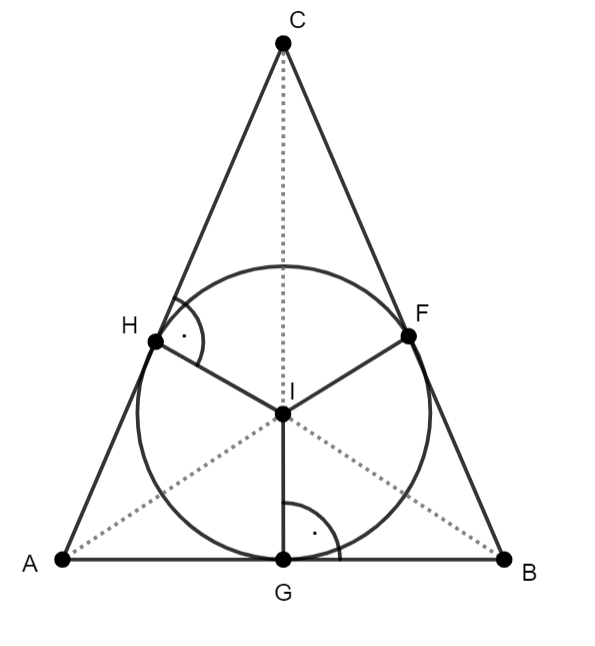
Trójkąt jest trójkątem równoramiennym.
Przyjmij:
|AC| = |BC| = 15 cm
|AB| = 18 cm
r–promień okręgu wpisanego w trójkąt
|HI| = |IG| = |IF|– = r
|CG|–wysokość trójkąta równoramiennego:
|AB| = |AG| + |GB|
|AB| = 2|GB|
18 = 2|GB| / 2
9 = GB
Trójkąt CGB
|CG|2 = |BC|2–|GB|2
|CG|2 = 152–92
|CG|2 = 225–81
|CG|2 = 144 |/√
|CG| = 12 cm
|CI| = |CG|–r
|CI| = 12–r
Metoda 1–Podobieństwo trójkątów
Zauważ, że trójkąty CHI i CGB są podobne: cecha kąt–kąt–kąt:
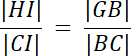
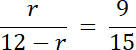
15r = 9∙(12–r)
15r = 108–9r | + 9r
24r = 108
r = 4,5 cm
Metoda 2–twierdzenie o odcinkach stycznych
|AG| = |AH| = 9 cm
|CH| = |AC|–|AG|
|CH| = 15–9 = 6 cm
|CH|2 + |HI|2 = |CI|2
62 + r2 = (12–r)2
36 + r2 = 144–24r + r2 |–r2
36 = 144–24r |–144
–108 = –24r |/(–24)
r = 4,5 cm

W tym zadaniu z twierdzenia Pitagorasa wyznacz wysokość trójkąta, a następnie skorzystaj z metody trójkątów podobnych (metoda I) i z twierdzenia o stycznych odcinkach (metoda II), aby wyznaczyć długość promienia okręgu wpisanego w trójkąt.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
