Mając dany ostrosłup prosty, którego podstawą jest kwadrat o boku a oraz wiedząc, że kąt, który tworzy krawędź boczna i krawędź podstawy, które początek mają w tym samym punkcie, jest równy 45° < α < 90°, określ objętość i sumę pól wszystkich ścian bryły.
Stwórz rysunek pomocniczy, gdzie H to wysokość ostrosłupa, a to krawędź podstawy, b to krawędź boczna, h to wysokość ściany bocznej, α to kąt podany w poleceniu:
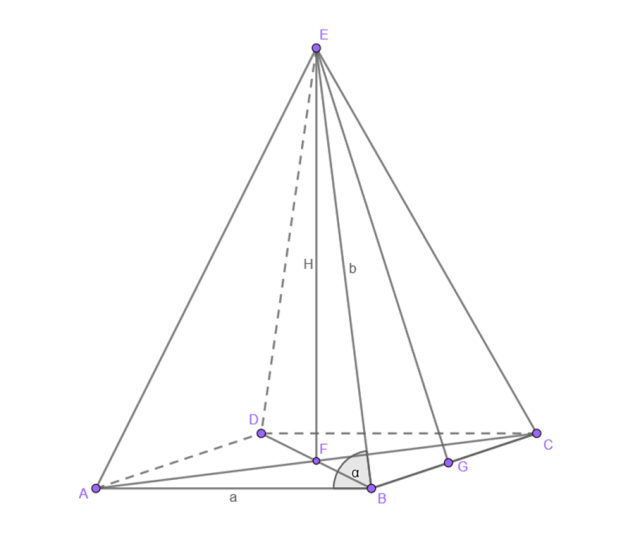
Uzależnij b od a korzystając z twierdzenia cosinusów:
![]()
![]()
![]()
![]()
Trójkąt ABE jest równoramienny. Oblicz jego wysokość h, korzystając z twierdzenia Pitagorasa:
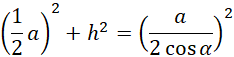
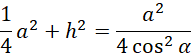
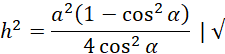
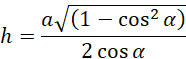
Oblicz pole powierzchni całkowitej:
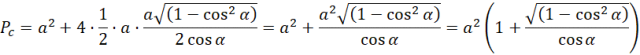
Skorzystaj ze wzoru na jedynkę trygonometryczną:
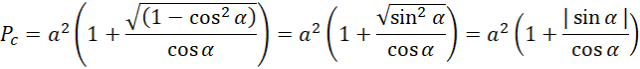
Skoro α ∈ (45°,90°) to i sinus i cosinus jest liczbą dodatnią, a więc:
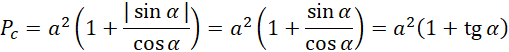
Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych, a więc BF jest równe połowie długości przekątnej podstawy.
Wykorzystaj twierdzenie Pitagorasa i oblicz H:
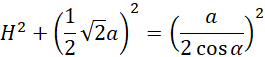
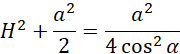
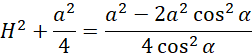
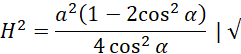
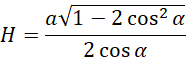
Oblicz objętość:
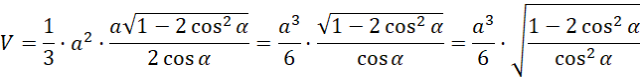
Wykorzystaj wzór na jedynkę trygonometryczną:
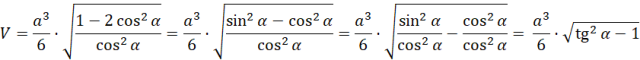

Stwórz rysunek pomocniczy. Najpierw wykorzystaj twierdzenie cosinusów
![]() do obliczenia b. Zauważ, że trójkąt ABE jest równoramienny, a więc jesteś w stanie obliczyć wysokość ściany bocznej, wykorzystując twierdzenie Pitagorasa. Następnie podstaw uzyskane dane do wzoru na pole powierzchni całkowitej i uprość otrzymany wynik. Wykorzystaj do tego wzór na jedynkę trygonometryczną
do obliczenia b. Zauważ, że trójkąt ABE jest równoramienny, a więc jesteś w stanie obliczyć wysokość ściany bocznej, wykorzystując twierdzenie Pitagorasa. Następnie podstaw uzyskane dane do wzoru na pole powierzchni całkowitej i uprość otrzymany wynik. Wykorzystaj do tego wzór na jedynkę trygonometryczną
![]() . Zauważ, że dla podanych wartości
. Zauważ, że dla podanych wartości
![]() sinus i cosinus są zawsze dodatnie. Następnie oblicz wysokość ostrosłupa, także korzystając z twierdzenia Pitagorasa. Podstaw uzyskane dane do wzoru na objętość ostrosłupa i uprość je, wykorzystując wzór na jedynkę trygonometryczną.
sinus i cosinus są zawsze dodatnie. Następnie oblicz wysokość ostrosłupa, także korzystając z twierdzenia Pitagorasa. Podstaw uzyskane dane do wzoru na objętość ostrosłupa i uprość je, wykorzystując wzór na jedynkę trygonometryczną.

Zadanie 5.1.
111Zadanie 5.2.
111Zadanie 5.4.
111Zadanie 5.5.
111Zadanie 5.6.
112Zadanie 5.7.
112Zadanie 5.8.
112Zadanie 5.37.
117Zadanie 5.39.
117Zadanie 5.41.
118Zadanie 5.42.
118Zadanie 5.43.
118Zadanie 5.46.
119Zadanie 5.49.
119Zadanie 5.50.
119Zadanie 5.51.
119Zadanie 5.54.
120Zadanie 5.60.
121Zadanie 5.62.
121Zadanie 5.63.
121Zadanie 5.64.
121Zadanie 5.65.
121Zadanie 5.67.
122Zadanie 5.69.
122Zadanie 5.70.
122Zadanie 5.71.
122Zadanie 5.72.
122Zadanie 5.73.
122Zadanie 5.74.
122Zadanie 5.75.
123Zadanie 5.76.
123Zadanie 5.77.
123Zadanie 5.78.
123Zadanie 5.79.
123Zadanie 5.80.
123Zadanie 5.81.
123Zadanie 5.82.
124Zadanie 5.83.
124Zadanie 5.84.
124Zadanie 5.85.
124Zadanie 5.86.
124Zadanie 5.87.
125Zadanie 5.88.
125Zadanie 5.91.
125Zadanie 5.92.
125Zadanie 5.93.
126Zadanie 5.95.
126Zadanie 5.96.
126Zadanie 5.97.
126Zadanie 5.98.
127Zadanie 5.110.
128Zadanie 5.112.
128Zadanie 5.121.
129Zadanie 5.126.
130Zadanie 5.133.
131Zadanie 5.134.
131Zadanie 5.136.
131Zadanie 5.141.
132Zadanie 5.144.
132Zadanie 5.145.
132Zadanie 5.148.
133Zadanie 5.155.
134Zadanie 5.156.
134Zadanie 5.157.
134Zadanie 5.158.
135Zadanie 5.159.
135Zadanie 5.160.
135Zadanie 5.170.
136Zadanie 5.172.
137Zadanie 5.185.
138Zadanie 18.
141Zadanie 19.
141Zadanie 20.
141Zadanie 21.
141Zadanie 24.
142Zadanie 25.
142Zadanie 27.
142Zadanie 29.
142Zadanie 30.
143Zadanie 32.
143
