Mając dany trójkąt, który jest podstawą graniastosłupa prostego oraz wiedząc, że na ścianach tej bryły zaznaczono punkty przecięcia się przekątnych, a następnie połączono je z wierzchołkami leżącymi naprzeciw danej ściany, udowodnij, że powstałe w ten sposób odcinki mają jeden punkt wspólny, dzielący je tak, że jedna część odcinka jest dwa razy dłuższa od drugiej.
Stwórz rysunek pomocniczy:
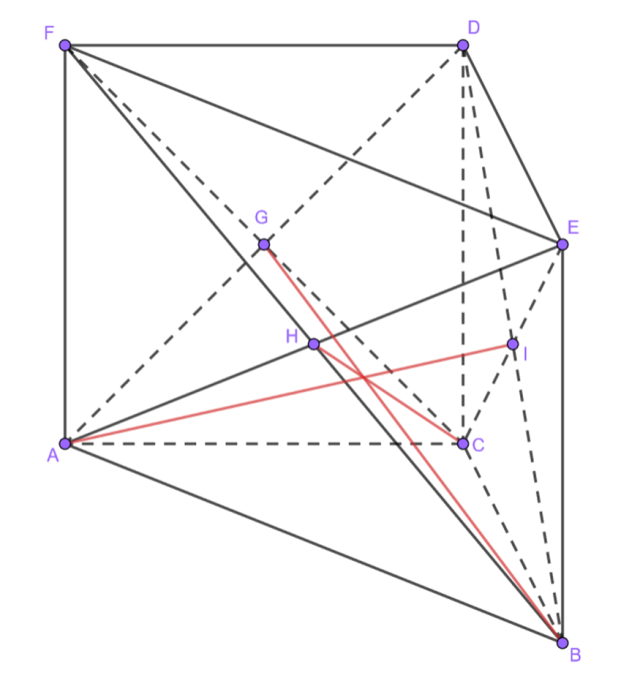
Zauważ, że przekątne w prostokącie przecinają się w połowie.
Stąd wynika, że odcinki AI oraz BG są środkowymi trójkąta ABD.
Zauważ, że taka sama sytuacja występuje w trójkącie BCF, w którym środkowymi są odcinki CH oraz BG.
Pamiętaj, że w dowolnym trójkącie środkowe przecinają się w stosunku 1 : 2, oznacza to, że AI oraz BG i CH oraz BG przecinają się w stosunku 1 : 2.
Środkowa BG powtórzyła się 2 razy, a nie może być ona podzielona w stosunku 1 : 2, w dwóch różnych miejscach. Oznacza to, że wszystkie te odcinki przecinają się w stosunku 1 : 2.
Co należało udowodnić.

Aby poprowadzić ten dowód, musisz wykorzystać twierdzenie mówiące o tym, że środkowe w trójkącie przecinają się w stosunku 1 : 2. Co więcej, aby udowodnić, że te odcinki są środkowe, wykorzystaj informację, że przekątne w prostokącie przecinają się w połowie. Oznacza to, że w trójkącie BCF środkowymi są odcinki CH oraz BG, a w trójkącie ABD - AI oraz BG. Zauważ, że odcinek BG powtarza się dwa razy i z dwoma różnymi odcinkami przecina się w stosunku 1 : 2, oznacza to, że tamte dwa odcinki też muszą się przecinać w tym samym punkcie, z tym samym stosunkiem.

Zadanie 5.1.
111Zadanie 5.2.
111Zadanie 5.4.
111Zadanie 5.5.
111Zadanie 5.6.
112Zadanie 5.7.
112Zadanie 5.8.
112Zadanie 5.37.
117Zadanie 5.39.
117Zadanie 5.41.
118Zadanie 5.42.
118Zadanie 5.43.
118Zadanie 5.46.
119Zadanie 5.49.
119Zadanie 5.50.
119Zadanie 5.51.
119Zadanie 5.54.
120Zadanie 5.60.
121Zadanie 5.62.
121Zadanie 5.63.
121Zadanie 5.64.
121Zadanie 5.65.
121Zadanie 5.67.
122Zadanie 5.69.
122Zadanie 5.70.
122Zadanie 5.71.
122Zadanie 5.72.
122Zadanie 5.73.
122Zadanie 5.74.
122Zadanie 5.75.
123Zadanie 5.76.
123Zadanie 5.77.
123Zadanie 5.78.
123Zadanie 5.79.
123Zadanie 5.80.
123Zadanie 5.81.
123Zadanie 5.82.
124Zadanie 5.83.
124Zadanie 5.84.
124Zadanie 5.85.
124Zadanie 5.86.
124Zadanie 5.87.
125Zadanie 5.88.
125Zadanie 5.91.
125Zadanie 5.92.
125Zadanie 5.93.
126Zadanie 5.95.
126Zadanie 5.96.
126Zadanie 5.97.
126Zadanie 5.98.
127Zadanie 5.110.
128Zadanie 5.112.
128Zadanie 5.121.
129Zadanie 5.126.
130Zadanie 5.133.
131Zadanie 5.134.
131Zadanie 5.136.
131Zadanie 5.141.
132Zadanie 5.144.
132Zadanie 5.145.
132Zadanie 5.148.
133Zadanie 5.155.
134Zadanie 5.156.
134Zadanie 5.157.
134Zadanie 5.158.
135Zadanie 5.159.
135Zadanie 5.160.
135Zadanie 5.170.
136Zadanie 5.172.
137Zadanie 5.185.
138Zadanie 18.
141Zadanie 19.
141Zadanie 20.
141Zadanie 21.
141Zadanie 24.
142Zadanie 25.
142Zadanie 27.
142Zadanie 29.
142Zadanie 30.
143Zadanie 32.
143
