Wiedząc, że odcinki A, B, C są współpłaszczyznowe i tworzą trójkąt prostokątny, wysokość opuszczona na punkt D z wierzchołka C dzieli bok na odcinki długości |AD| = 9 cm i |DB| = 4 cm, odcinek EC tworzy kąt prosty z płaszczyzną zawierającą wspomniane wcześniej punkty oraz PABC = PABE – 26 cm2, wyznacz długość odcinka EC.
Na początku stwórz rysunek pomocniczy:
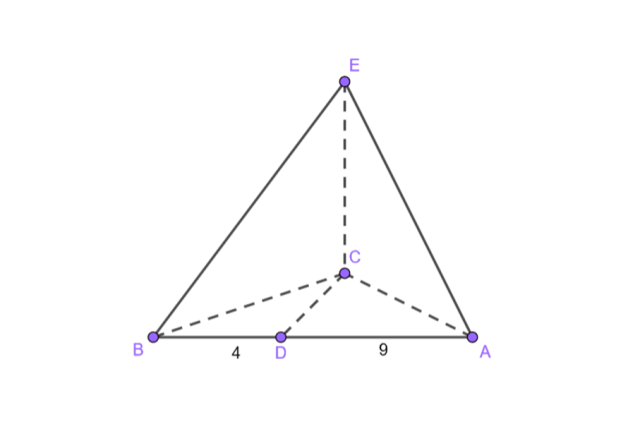 Wykorzystaj twierdzenie o trzech prostych prostopadłych.
Wykorzystaj twierdzenie o trzech prostych prostopadłych.
Zauważ, że rzutem prostopadłym odcinka DE jest odcinek CD. Odcinek AB oraz DE są prostopadłe, a więc odcinek DE też musi być prostopadły do AB. A więc odcinek DE jest wysokością trójkąta ABE.
Wykorzystaj wzór na wysokość w trójkącie prostokątnym
![]() :
:
![]()
![]()
![]()
Oblicz pole ABC:
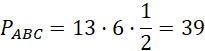
Oblicz pole ABE:
![]()
Oblicz długość odcinka DE, wykorzystując pole ABE:
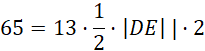
![]()
![]()
Za pomocą twierdzenia Pitagorasa oblicz długość odcinka CE:
![]()
![]()
![]()
![]()

Zauważ, że możesz wykazać, że odcinek DE jest prostopadły do AB. Aby to zrobić, musisz wykorzystać twierdzenie o trzech prostych prostopadłych mówiące, że jak rzut prostopadły prostej k jest prostopadły do pewnej prostej m to prosta k też musi być prostopadła do prostej m. W tym przypadku prostą k jest odcinek DE, jego rzutem jest odcinek CD, a rolę prostej m odgrywa odcinek AB. Odcinki AB oraz CD są prostopadłe do siebie, ponieważ tak wynika z treści zadania, dlatego odcinek DE też jest prostopadły do AB, a więc DE jest wysokością trójkąta ABE. Oblicz długość odcinka CD korzystając ze wzoru na wysokość opuszczoną na przeciwprostokątną w trójkącie prostokątnym
![]() . Oblicz pole ABC, a następnie wyznacz pole ABE. Z pola ABE wyznacz długość odcinka DE. Wykorzystując twierdzenie Pitagorasa oblicz długość CE.
. Oblicz pole ABC, a następnie wyznacz pole ABE. Z pola ABE wyznacz długość odcinka DE. Wykorzystując twierdzenie Pitagorasa oblicz długość CE.

Zadanie 5.1.
111Zadanie 5.2.
111Zadanie 5.4.
111Zadanie 5.5.
111Zadanie 5.6.
112Zadanie 5.7.
112Zadanie 5.8.
112Zadanie 5.37.
117Zadanie 5.39.
117Zadanie 5.41.
118Zadanie 5.42.
118Zadanie 5.43.
118Zadanie 5.46.
119Zadanie 5.49.
119Zadanie 5.50.
119Zadanie 5.51.
119Zadanie 5.54.
120Zadanie 5.60.
121Zadanie 5.62.
121Zadanie 5.63.
121Zadanie 5.64.
121Zadanie 5.65.
121Zadanie 5.67.
122Zadanie 5.69.
122Zadanie 5.70.
122Zadanie 5.71.
122Zadanie 5.72.
122Zadanie 5.73.
122Zadanie 5.74.
122Zadanie 5.75.
123Zadanie 5.76.
123Zadanie 5.77.
123Zadanie 5.78.
123Zadanie 5.79.
123Zadanie 5.80.
123Zadanie 5.81.
123Zadanie 5.82.
124Zadanie 5.83.
124Zadanie 5.84.
124Zadanie 5.85.
124Zadanie 5.86.
124Zadanie 5.87.
125Zadanie 5.88.
125Zadanie 5.91.
125Zadanie 5.92.
125Zadanie 5.93.
126Zadanie 5.95.
126Zadanie 5.96.
126Zadanie 5.97.
126Zadanie 5.98.
127Zadanie 5.110.
128Zadanie 5.112.
128Zadanie 5.121.
129Zadanie 5.126.
130Zadanie 5.133.
131Zadanie 5.134.
131Zadanie 5.136.
131Zadanie 5.141.
132Zadanie 5.144.
132Zadanie 5.145.
132Zadanie 5.148.
133Zadanie 5.155.
134Zadanie 5.156.
134Zadanie 5.157.
134Zadanie 5.158.
135Zadanie 5.159.
135Zadanie 5.160.
135Zadanie 5.170.
136Zadanie 5.172.
137Zadanie 5.185.
138Zadanie 18.
141Zadanie 19.
141Zadanie 20.
141Zadanie 21.
141Zadanie 24.
142Zadanie 25.
142Zadanie 27.
142Zadanie 29.
142Zadanie 30.
143Zadanie 32.
143
