Mając dany trójkąt prostokątny, w którym dwa najkrótsze boki wynoszą 6 i 8 oraz wiedząc, że jest on podstawą ostrosłupa, którego ściany tworzą z podstawą kąt dwuścienny ostry
![]() , spełniający równość
, spełniający równość
![]() , wyznacz, ile mają krawędzie boczne tej bryły.
, wyznacz, ile mają krawędzie boczne tej bryły.
Stwórz rysunek pomocniczy, gdzie BC jest przeciwprostokątną podstawy, a zaznaczone kąty mają taką samą miarę:
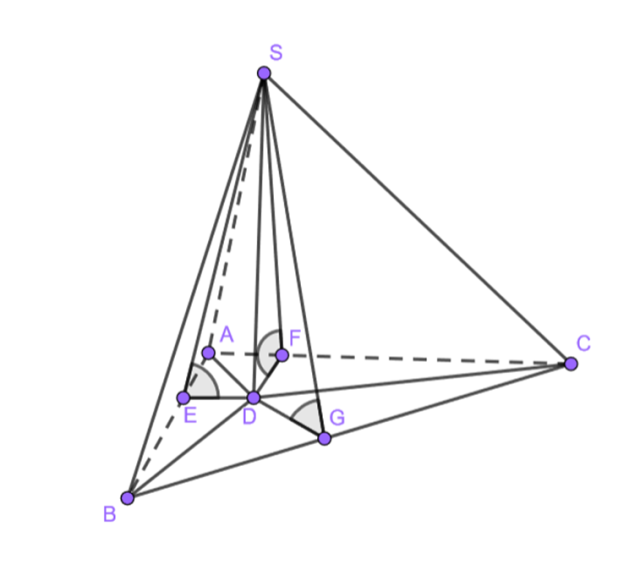
Wykorzystaj obliczone długości odcinka BC, promienia r oraz wysokości DS, z poprzedniego podpunktu.
Promień tworzy kąt prosty z odcinkiem, z którym się łączy.
Czworokąt AFED jest kwadratem.
Oblicz długość odcinka EB:
![]()
![]()
Wykorzystaj twierdzenie Pitagorasa i oblicz długość BD:
![]()
![]()
![]()
![]()
Wykorzystaj twierdzenie Pitagorasa i oblicz długość krawędzi bocznej BS:
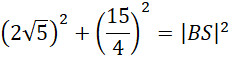
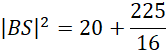
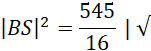
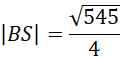
Oblicz długość odcinka AD:
![]()
![]()
Wykorzystaj twierdzenie Pitagorasa i oblicz długość krawędzi bocznej AS:
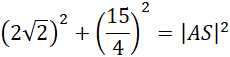
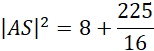
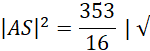
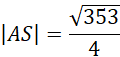
Oblicz długość odcinka CF:
![]()
![]()
Wykorzystaj twierdzenie Pitagorasa i oblicz długość CD:
![]()
![]()
![]()
![]()
Wykorzystaj twierdzenie Pitagorasa i oblicz długość krawędzi bocznej CS:
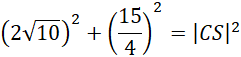
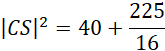
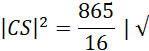
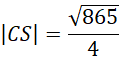

Pamiętaj, że jeśli ściany boczne są nachylone pod takim samym kątem do podstawy, to w podstawę można wpisać okrąg. W podpunkcie a) została obliczona długość odcinka BC, promień r oraz wysokość DS, skorzystaj z tego. Zauważ, że promienie okręgu wpisanego tworzą kąt prosty z bokami trójkąta, a więc czworokąt AFDE jest kwadratem, ponieważ kąty przy wierzchołkach F i E są proste oraz kąt przy wierzchołku A jest prosty.
Aby obliczyć długość krawędzi BS musisz najpierw obliczyć długość odcinka EB. Wystarczy, że od długości przyprostokątnej AB odejmiesz długość promienia. Następnie wykorzystaj twierdzenie Pitagorasa do obliczenia długości BD, a potem znowu skorzystaj z tego twierdzenia do obliczenia długości BS.
Aby obliczyć długość krawędzi AS musisz najpierw obliczyć długość odcinka AD, a skoro AFDE jest kwadratem, to AD ma długość
![]() , gdzie a to bok kwadratu. Następnie wykorzystaj twierdzenie Pitagorasa do obliczenia długości AS.
, gdzie a to bok kwadratu. Następnie wykorzystaj twierdzenie Pitagorasa do obliczenia długości AS.
Aby obliczyć długość krawędzi CS musisz najpierw obliczyć długość odcinka FC. Wystarczy, że od długości przyprostokątnej AC odejmiesz długość promienia. Następnie wykorzystaj twierdzenie Pitagorasa do obliczenia długości CD, a potem znowu skorzystaj z tego twierdzenia do obliczenia długości CS.

Zadanie 5.1.
111Zadanie 5.2.
111Zadanie 5.4.
111Zadanie 5.5.
111Zadanie 5.6.
112Zadanie 5.7.
112Zadanie 5.8.
112Zadanie 5.37.
117Zadanie 5.39.
117Zadanie 5.41.
118Zadanie 5.42.
118Zadanie 5.43.
118Zadanie 5.46.
119Zadanie 5.49.
119Zadanie 5.50.
119Zadanie 5.51.
119Zadanie 5.54.
120Zadanie 5.60.
121Zadanie 5.62.
121Zadanie 5.63.
121Zadanie 5.64.
121Zadanie 5.65.
121Zadanie 5.67.
122Zadanie 5.69.
122Zadanie 5.70.
122Zadanie 5.71.
122Zadanie 5.72.
122Zadanie 5.73.
122Zadanie 5.74.
122Zadanie 5.75.
123Zadanie 5.76.
123Zadanie 5.77.
123Zadanie 5.78.
123Zadanie 5.79.
123Zadanie 5.80.
123Zadanie 5.81.
123Zadanie 5.82.
124Zadanie 5.83.
124Zadanie 5.84.
124Zadanie 5.85.
124Zadanie 5.86.
124Zadanie 5.87.
125Zadanie 5.88.
125Zadanie 5.91.
125Zadanie 5.92.
125Zadanie 5.93.
126Zadanie 5.95.
126Zadanie 5.96.
126Zadanie 5.97.
126Zadanie 5.98.
127Zadanie 5.110.
128Zadanie 5.112.
128Zadanie 5.121.
129Zadanie 5.126.
130Zadanie 5.133.
131Zadanie 5.134.
131Zadanie 5.136.
131Zadanie 5.141.
132Zadanie 5.144.
132Zadanie 5.145.
132Zadanie 5.148.
133Zadanie 5.155.
134Zadanie 5.156.
134Zadanie 5.157.
134Zadanie 5.158.
135Zadanie 5.159.
135Zadanie 5.160.
135Zadanie 5.170.
136Zadanie 5.172.
137Zadanie 5.185.
138Zadanie 18.
141Zadanie 19.
141Zadanie 20.
141Zadanie 21.
141Zadanie 24.
142Zadanie 25.
142Zadanie 27.
142Zadanie 29.
142Zadanie 30.
143Zadanie 32.
143
