Dany jest pewien ostrosłup prawidłowy trójkątny ABCD. Przez bryłę przeprowadzono płaszczyznę w taki sposób, że zawiera ona odcinek AB podstawy oraz punkt S będący środkiem krawędzi bocznej CD. Płaszczyzna ta tworzy również z płaszczyzną podstawy kąt o mierze 45°. Oblicz cosinus kąta ASB.
Naszkicuj sytuację przedstawioną w treści zadania:
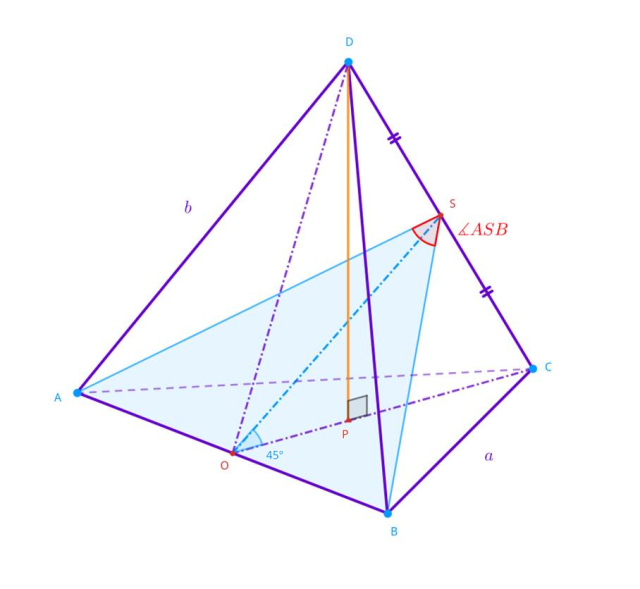
Oznacz długość krawędzi podstawy jako 𝑎, a długość krawędzi bocznej jako 𝑏. Zauważ, że odcinek OC to wysokość trójkąta równobocznego, zatem wynosi ona:
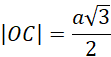
Spodek wysokości P dzieli wysokość podstawy ostrosłupa na odcinki o długościach w stosunku 2 : 1. Długość odcinka PC wynosi:
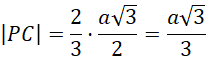
Oblicz cosinus kąta PCD, korzystając z definicji funkcji trygonometrycznych w trójkącie prostokątnym:
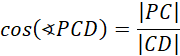
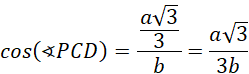
Oblicz sinus tego kąta za pomocą jedynki trygonometrycznej:
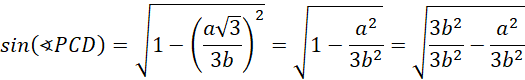
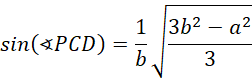
Oblicz długość odcinka BS, środkowej trójkąta DBC:
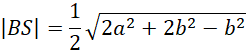
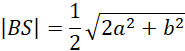
Oblicz wysokość przekroju OS:
![]()
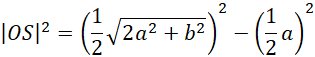
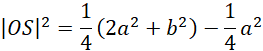
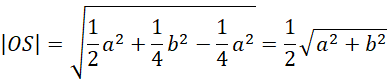
Skorzystaj z twierdzenia sinusów, żeby uzależnić długość krawędzi podstawy od długości krawędzi bocznej:
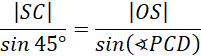
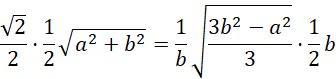
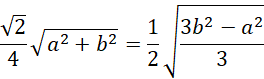
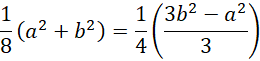
![]()
![]()
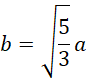
Zatem długość odcinka BS wynosi:
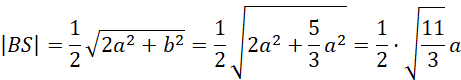
Skorzystaj z twierdzenia cosinusów, by wyznaczyć cosinus kąta ASB:
![]()
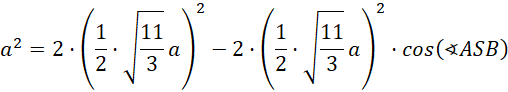
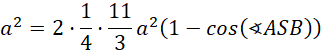
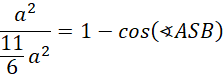
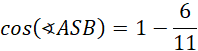
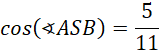

Oznacz długość krawędzi podstawy jako 𝑎, a długość krawędzi bocznej jako 𝑏. Oblicz długość odcinka łączącego spodek wysokości bryły z wierzchołkiem podstawy, a następnie oblicz sinus kąta między krawędzią boczną a płaszczyzną podstawy za pomocą definicji funkcji trygonometrycznych oraz jedynki trygonometrycznej:
![]()
Zauważ, że ramię powstałego przekroju to środkowa ściany bocznej DBC. Skorzystaj ze wzoru na długość środkowej trójkąta:
![]()
gdzie 𝑎, 𝑏 i 𝑐 to długości boków trójkąta, a środkowa 𝑑 opada na bok 𝑐.
Oblicz wysokość przekroju za pomocą twierdzenia Pitagorasa i skorzystaj z twierdzenia sinusów w trójkącie OSC, by uzależnić długość krawędzi podstawy od krawędzi bocznej.
Wstaw obliczoną relację do wzoru na długość ramienia przekroju BS. Wreszcie, użyj twierdzenia cosinusów w przekroju, by wyznaczyć cosinus kąta ASB.

Zadanie 5.1.
111Zadanie 5.2.
111Zadanie 5.4.
111Zadanie 5.5.
111Zadanie 5.6.
112Zadanie 5.7.
112Zadanie 5.8.
112Zadanie 5.37.
117Zadanie 5.39.
117Zadanie 5.41.
118Zadanie 5.42.
118Zadanie 5.43.
118Zadanie 5.46.
119Zadanie 5.49.
119Zadanie 5.50.
119Zadanie 5.51.
119Zadanie 5.54.
120Zadanie 5.60.
121Zadanie 5.62.
121Zadanie 5.63.
121Zadanie 5.64.
121Zadanie 5.65.
121Zadanie 5.67.
122Zadanie 5.69.
122Zadanie 5.70.
122Zadanie 5.71.
122Zadanie 5.72.
122Zadanie 5.73.
122Zadanie 5.74.
122Zadanie 5.75.
123Zadanie 5.76.
123Zadanie 5.77.
123Zadanie 5.78.
123Zadanie 5.79.
123Zadanie 5.80.
123Zadanie 5.81.
123Zadanie 5.82.
124Zadanie 5.83.
124Zadanie 5.84.
124Zadanie 5.85.
124Zadanie 5.86.
124Zadanie 5.87.
125Zadanie 5.88.
125Zadanie 5.91.
125Zadanie 5.92.
125Zadanie 5.93.
126Zadanie 5.95.
126Zadanie 5.96.
126Zadanie 5.97.
126Zadanie 5.98.
127Zadanie 5.110.
128Zadanie 5.112.
128Zadanie 5.121.
129Zadanie 5.126.
130Zadanie 5.133.
131Zadanie 5.134.
131Zadanie 5.136.
131Zadanie 5.141.
132Zadanie 5.144.
132Zadanie 5.145.
132Zadanie 5.148.
133Zadanie 5.155.
134Zadanie 5.156.
134Zadanie 5.157.
134Zadanie 5.158.
135Zadanie 5.159.
135Zadanie 5.160.
135Zadanie 5.170.
136Zadanie 5.172.
137Zadanie 5.185.
138Zadanie 18.
141Zadanie 19.
141Zadanie 20.
141Zadanie 21.
141Zadanie 24.
142Zadanie 25.
142Zadanie 27.
142Zadanie 29.
142Zadanie 30.
143Zadanie 32.
143
