Dany jest pewien ostrosłup prawidłowy czworokątny o wszystkich krawędziach przystających i długości 𝑎. Przez bryłę przeprowadzono płaszczyznę w taki sposób, że zawiera ona środki dwóch sąsiadujących krawędzi bocznych oraz wysokości. Oblicz pole otrzymanego przekroju.
Naszkicuj sytuację przedstawioną w treści zadania:
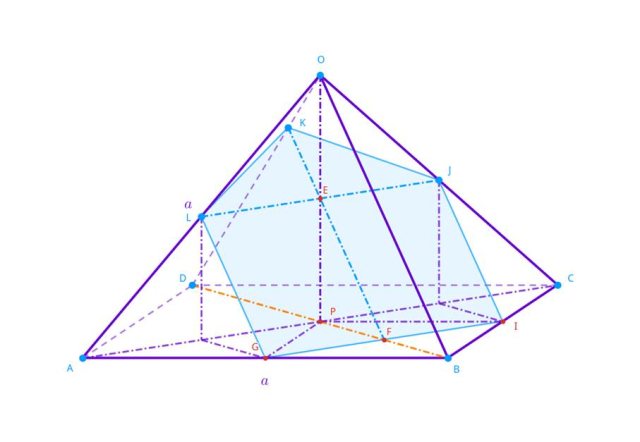
By wyznaczyć pole przekroju GIJKL, potrzebna będzie długość odcinka EF, KE oraz odcinka GI.
Spodek wysokości P w ostrosłupie prawidłowym czworokątnym jest środkiem symetrii podstawy. Zauważ, że odcinek GP i PI mają tę samą długość równą połowie długości krawędzi bocznej i tworzą kwadrat GPIB o boku długości
![]() cm. Odcinek GI jest przekątną tego kwadratu, więc ma długość:
cm. Odcinek GI jest przekątną tego kwadratu, więc ma długość:
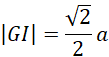
Zauważ, że trójkąt EPF jest podobny do trójkąta OPB w skali
![]() (bok-kąt-bok). Mamy więc:
(bok-kąt-bok). Mamy więc:
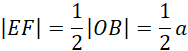
Trójkąt DFK jest podobny do trójkąta DBO
![]() . Skala podobieństwa wynosi:
. Skala podobieństwa wynosi:
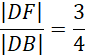
Wobec tego:
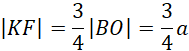
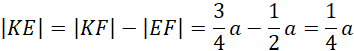
Oblicz pole przekroju:
![]()
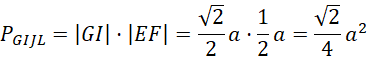
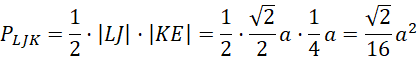
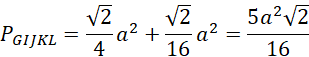

Wykorzystaj długości charakterystycznych odcinków (przekątna kwadratu, własności ostrosłupów prawidłowych) oraz podobieństwo figur, by obliczyć długości odpowiednich odcinków przekroju, znając tylko długość krawędzi.

Zadanie 5.1.
111Zadanie 5.2.
111Zadanie 5.4.
111Zadanie 5.5.
111Zadanie 5.6.
112Zadanie 5.7.
112Zadanie 5.8.
112Zadanie 5.37.
117Zadanie 5.39.
117Zadanie 5.41.
118Zadanie 5.42.
118Zadanie 5.43.
118Zadanie 5.46.
119Zadanie 5.49.
119Zadanie 5.50.
119Zadanie 5.51.
119Zadanie 5.54.
120Zadanie 5.60.
121Zadanie 5.62.
121Zadanie 5.63.
121Zadanie 5.64.
121Zadanie 5.65.
121Zadanie 5.67.
122Zadanie 5.69.
122Zadanie 5.70.
122Zadanie 5.71.
122Zadanie 5.72.
122Zadanie 5.73.
122Zadanie 5.74.
122Zadanie 5.75.
123Zadanie 5.76.
123Zadanie 5.77.
123Zadanie 5.78.
123Zadanie 5.79.
123Zadanie 5.80.
123Zadanie 5.81.
123Zadanie 5.82.
124Zadanie 5.83.
124Zadanie 5.84.
124Zadanie 5.85.
124Zadanie 5.86.
124Zadanie 5.87.
125Zadanie 5.88.
125Zadanie 5.91.
125Zadanie 5.92.
125Zadanie 5.93.
126Zadanie 5.95.
126Zadanie 5.96.
126Zadanie 5.97.
126Zadanie 5.98.
127Zadanie 5.110.
128Zadanie 5.112.
128Zadanie 5.121.
129Zadanie 5.126.
130Zadanie 5.133.
131Zadanie 5.134.
131Zadanie 5.136.
131Zadanie 5.141.
132Zadanie 5.144.
132Zadanie 5.145.
132Zadanie 5.148.
133Zadanie 5.155.
134Zadanie 5.156.
134Zadanie 5.157.
134Zadanie 5.158.
135Zadanie 5.159.
135Zadanie 5.160.
135Zadanie 5.170.
136Zadanie 5.172.
137Zadanie 5.185.
138Zadanie 18.
141Zadanie 19.
141Zadanie 20.
141Zadanie 21.
141Zadanie 24.
142Zadanie 25.
142Zadanie 27.
142Zadanie 29.
142Zadanie 30.
143Zadanie 32.
143
