Udowodnij, że PQ jest równoległa do płaszczyzny π, gdy |AP| ⋅ |CQ| = |PC| ⋅ |BQ| oraz wiedząc, że A i B znajdują się na płaszczyźnie π, C to punkt znajdujący się w przestrzeni, ale nienależący do płaszczyzny π, a P i Q należą odpowiednio do odcinków AC oraz BC.
Rysunek obrazujący sytuację z polecenia:
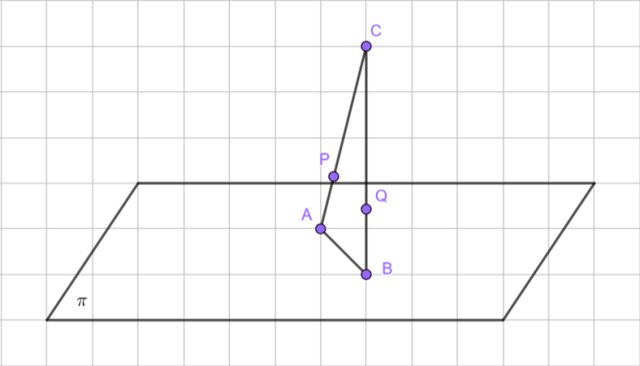
Przekształć podane równanie:
![]()
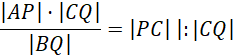
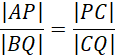
Zauważ, że podana równość spełnia założenia twierdzenia odwrotnego do twierdzenia Talesa, a więc odcinki PQ oraz AB są równoległe.
Jeśli odcinki PQ oraz AB są równoległe, a punkty A i B zawierają się na płaszczyźnie, to i odcinek AB zawiera się w płaszczyźnie π. Oznacza to, że odcinek PQ jest równoległy do płaszczyzny π.
Co kończy dowód.

Zauważ, że do udowodnienia podanego zadania musisz wykorzystać twierdzenie odwrotne do twierdzenia Talesa, które mówi, że jeśli stosunki odpowiadających sobie odcinków, przy pewnym kącie, są sobie równe, to proste przecinające ramiona tego kąta są równoległe. Przekształć podane równanie tak, aby otrzymać stosunki spełniające założenia przywołanego twierdzenia.

Zadanie 5.1.
111Zadanie 5.2.
111Zadanie 5.4.
111Zadanie 5.5.
111Zadanie 5.6.
112Zadanie 5.7.
112Zadanie 5.8.
112Zadanie 5.37.
117Zadanie 5.39.
117Zadanie 5.41.
118Zadanie 5.42.
118Zadanie 5.43.
118Zadanie 5.46.
119Zadanie 5.49.
119Zadanie 5.50.
119Zadanie 5.51.
119Zadanie 5.54.
120Zadanie 5.60.
121Zadanie 5.62.
121Zadanie 5.63.
121Zadanie 5.64.
121Zadanie 5.65.
121Zadanie 5.67.
122Zadanie 5.69.
122Zadanie 5.70.
122Zadanie 5.71.
122Zadanie 5.72.
122Zadanie 5.73.
122Zadanie 5.74.
122Zadanie 5.75.
123Zadanie 5.76.
123Zadanie 5.77.
123Zadanie 5.78.
123Zadanie 5.79.
123Zadanie 5.80.
123Zadanie 5.81.
123Zadanie 5.82.
124Zadanie 5.83.
124Zadanie 5.84.
124Zadanie 5.85.
124Zadanie 5.86.
124Zadanie 5.87.
125Zadanie 5.88.
125Zadanie 5.91.
125Zadanie 5.92.
125Zadanie 5.93.
126Zadanie 5.95.
126Zadanie 5.96.
126Zadanie 5.97.
126Zadanie 5.98.
127Zadanie 5.110.
128Zadanie 5.112.
128Zadanie 5.121.
129Zadanie 5.126.
130Zadanie 5.133.
131Zadanie 5.134.
131Zadanie 5.136.
131Zadanie 5.141.
132Zadanie 5.144.
132Zadanie 5.145.
132Zadanie 5.148.
133Zadanie 5.155.
134Zadanie 5.156.
134Zadanie 5.157.
134Zadanie 5.158.
135Zadanie 5.159.
135Zadanie 5.160.
135Zadanie 5.170.
136Zadanie 5.172.
137Zadanie 5.185.
138Zadanie 18.
141Zadanie 19.
141Zadanie 20.
141Zadanie 21.
141Zadanie 24.
142Zadanie 25.
142Zadanie 27.
142Zadanie 29.
142Zadanie 30.
143Zadanie 32.
143
