Mając dany ostrosłup, którego podstawą jest romb ABCD, w którym wysokość opuszczona z wierzchołka kąta rozwartego dzieli odcinek AB na odcinki AE oraz EB o długościach odpowiednio 6 i 4 oraz wiedząc, że kąt dwuścienny pomiędzy podstawą, a każdą ścianą boczną jest taki sam, a suma pól ścian bocznych ma 170, określ wysokość bryły.
Jeśli kąt dwuścienny pomiędzy podstawą, a ścianami bocznymi jest taki sam to w podstawę ostrosłupa można wpisać okrąg, a spodek wysokości pokrywa się ze środkiem okręgu.
Stwórz rysunek pomocniczy, gdzie H to wysokość ostrosłupa, r to promień okręgu wpisanego w podstawę, h to wysokość ściany bocznej, α to kąt pomiędzy ścianą boczną i podstawą:
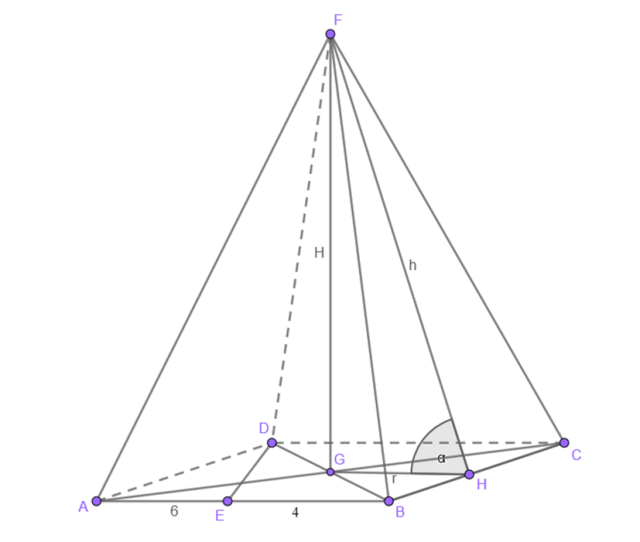
Oblicz pole powierzchni jednej ściany bocznej:
![]()
Oblicz h:
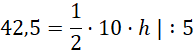
![]()
Trójkąt ADE jest trójkątem prostokątnym. Oblicz długość DE, korzystając z twierdzenia Pitagorasa:
![]()
![]()
![]()
![]()
Dwa promienie są wysokością rombu. Oblicz długość r:
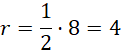
Wykorzystaj twierdzenie Pitagorasa do obliczenia H:
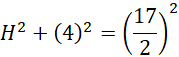
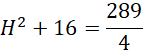
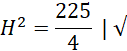
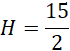

Zauważ, że w podstawę ostrosłupa można wpisać okrąg i środek tego okręgu będzie spodkiem wysokości, jeśli kąt dwuścienny pomiędzy podstawą, a ścianami bocznymi jest taki sam. Stwórz rysunek pomocniczy. Najpierw oblicz pole jednej ściany, korzystając z podanego pola powierzchni bocznej. Następnie oblicz h, korzystając z pola jednej ściany bocznej. Zauważ, że trójkąt AED jest trójkątem prostokątny, a więc możesz obliczyć DE korzystając z twierdzenia Pitagorasa. Dodatkowo zwróć uwagę na to, że wysokość podstawy wynosi tyle samo co dwa promienie okręgu wpisanego, więc oblicz r. Na koniec wykorzystaj twierdzenie Pitagorasa do obliczenia H.

Zadanie 5.1.
111Zadanie 5.2.
111Zadanie 5.4.
111Zadanie 5.5.
111Zadanie 5.6.
112Zadanie 5.7.
112Zadanie 5.8.
112Zadanie 5.37.
117Zadanie 5.39.
117Zadanie 5.41.
118Zadanie 5.42.
118Zadanie 5.43.
118Zadanie 5.46.
119Zadanie 5.49.
119Zadanie 5.50.
119Zadanie 5.51.
119Zadanie 5.54.
120Zadanie 5.60.
121Zadanie 5.62.
121Zadanie 5.63.
121Zadanie 5.64.
121Zadanie 5.65.
121Zadanie 5.67.
122Zadanie 5.69.
122Zadanie 5.70.
122Zadanie 5.71.
122Zadanie 5.72.
122Zadanie 5.73.
122Zadanie 5.74.
122Zadanie 5.75.
123Zadanie 5.76.
123Zadanie 5.77.
123Zadanie 5.78.
123Zadanie 5.79.
123Zadanie 5.80.
123Zadanie 5.81.
123Zadanie 5.82.
124Zadanie 5.83.
124Zadanie 5.84.
124Zadanie 5.85.
124Zadanie 5.86.
124Zadanie 5.87.
125Zadanie 5.88.
125Zadanie 5.91.
125Zadanie 5.92.
125Zadanie 5.93.
126Zadanie 5.95.
126Zadanie 5.96.
126Zadanie 5.97.
126Zadanie 5.98.
127Zadanie 5.110.
128Zadanie 5.112.
128Zadanie 5.121.
129Zadanie 5.126.
130Zadanie 5.133.
131Zadanie 5.134.
131Zadanie 5.136.
131Zadanie 5.141.
132Zadanie 5.144.
132Zadanie 5.145.
132Zadanie 5.148.
133Zadanie 5.155.
134Zadanie 5.156.
134Zadanie 5.157.
134Zadanie 5.158.
135Zadanie 5.159.
135Zadanie 5.160.
135Zadanie 5.170.
136Zadanie 5.172.
137Zadanie 5.185.
138Zadanie 18.
141Zadanie 19.
141Zadanie 20.
141Zadanie 21.
141Zadanie 24.
142Zadanie 25.
142Zadanie 27.
142Zadanie 29.
142Zadanie 30.
143Zadanie 32.
143
