Udowodnij, że proste S1S2 i S3S4 są do siebie równoległe, wiedząc, że punkty A, B, C, D, A1, B1, C1, D1 tworzą sześcian, na którego krawędziach znajdują się punkty P, Q, R, T, środkiem odcinka TP jest punkt S1, środkiem odcinka TQ – S2, środkiem odcinka RP – S3, a środkiem odcinka RQ – S4.
Wiadomo, że:
![]()
![]()
![]()
![]()
Zauważ, że możesz skorzystać z twierdzenia odwrotnego do twierdzenia Talesa, aby udowodnić równoległość odcinków S1S2 oraz PQ:
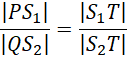
Zamień elementy po prawej stronie równości:
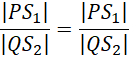
Oznacza to, że w kącie PTQ zachodzi twierdzenie odwrotne do twierdzenia Talesa, a więc odcinki PQ oraz S1S2 są równoległe.
Zauważ, że możesz skorzystać z twierdzenia odwrotnego do twierdzenia Talesa, aby udowodnić równoległość odcinków S3S4 oraz PQ:
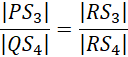
Zamień elementy po prawej stronie równości:
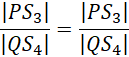
Oznacza to, że w kącie PRQ zachodzi twierdzenie odwrotne do twierdzenia Talesa, a więc odcinki PQ oraz S3S4 są równoległe.
Skoro odcinki S1S2 oraz S3S4 są równoległe do PQ to oznacza, że one też są równoległe ze sobą.
Co kończy dowód.

Wykorzystaj podany rysunek i zauważ, że możesz wykorzystać twierdzenie odwrotne do twierdzenia Talesa, które mówi, że jeśli stosunki odpowiadających sobie odcinków, przy pewnym kącie, są sobie równe, to proste przecinające ramiona tego kąta są równoległe. Stwórz proporcję
![]() i wykorzystaj to, że
i wykorzystaj to, że
![]() oraz
oraz
![]() . Podmień odpowiednie elementy proporcji. Twierdzenie jest spełnione, a więc odcinki S1S2 oraz PQ są równoległe. Analogicznie udowodnij równoległość odcinków S3S4 oraz PQ. Następnie zauważ, że skoro odcinki S1S2 oraz S3S4 są równoległe z odcinkiem PQ, to oznacza, że są także równoległe ze sobą.
. Podmień odpowiednie elementy proporcji. Twierdzenie jest spełnione, a więc odcinki S1S2 oraz PQ są równoległe. Analogicznie udowodnij równoległość odcinków S3S4 oraz PQ. Następnie zauważ, że skoro odcinki S1S2 oraz S3S4 są równoległe z odcinkiem PQ, to oznacza, że są także równoległe ze sobą.

Zadanie 5.1.
111Zadanie 5.2.
111Zadanie 5.4.
111Zadanie 5.5.
111Zadanie 5.6.
112Zadanie 5.7.
112Zadanie 5.8.
112Zadanie 5.37.
117Zadanie 5.39.
117Zadanie 5.41.
118Zadanie 5.42.
118Zadanie 5.43.
118Zadanie 5.46.
119Zadanie 5.49.
119Zadanie 5.50.
119Zadanie 5.51.
119Zadanie 5.54.
120Zadanie 5.60.
121Zadanie 5.62.
121Zadanie 5.63.
121Zadanie 5.64.
121Zadanie 5.65.
121Zadanie 5.67.
122Zadanie 5.69.
122Zadanie 5.70.
122Zadanie 5.71.
122Zadanie 5.72.
122Zadanie 5.73.
122Zadanie 5.74.
122Zadanie 5.75.
123Zadanie 5.76.
123Zadanie 5.77.
123Zadanie 5.78.
123Zadanie 5.79.
123Zadanie 5.80.
123Zadanie 5.81.
123Zadanie 5.82.
124Zadanie 5.83.
124Zadanie 5.84.
124Zadanie 5.85.
124Zadanie 5.86.
124Zadanie 5.87.
125Zadanie 5.88.
125Zadanie 5.91.
125Zadanie 5.92.
125Zadanie 5.93.
126Zadanie 5.95.
126Zadanie 5.96.
126Zadanie 5.97.
126Zadanie 5.98.
127Zadanie 5.110.
128Zadanie 5.112.
128Zadanie 5.121.
129Zadanie 5.126.
130Zadanie 5.133.
131Zadanie 5.134.
131Zadanie 5.136.
131Zadanie 5.141.
132Zadanie 5.144.
132Zadanie 5.145.
132Zadanie 5.148.
133Zadanie 5.155.
134Zadanie 5.156.
134Zadanie 5.157.
134Zadanie 5.158.
135Zadanie 5.159.
135Zadanie 5.160.
135Zadanie 5.170.
136Zadanie 5.172.
137Zadanie 5.185.
138Zadanie 18.
141Zadanie 19.
141Zadanie 20.
141Zadanie 21.
141Zadanie 24.
142Zadanie 25.
142Zadanie 27.
142Zadanie 29.
142Zadanie 30.
143Zadanie 32.
143
