Na trójkącie prostokątnym równoramiennym o ramieniu długości 10 zbudowano ostrosłup prosty. O dwóch przystających ścianach bryły wiadomo, że są one nachylone do płaszczyzny podstawy pod kątem, którego cosinus wynosi
![]() . Oblicz tangens kąta między krawędzią boczną a płaszczyzną podstawy tak powstałej bryły.
. Oblicz tangens kąta między krawędzią boczną a płaszczyzną podstawy tak powstałej bryły.
Naszkicuj sytuację przedstawioną w treści zadania:
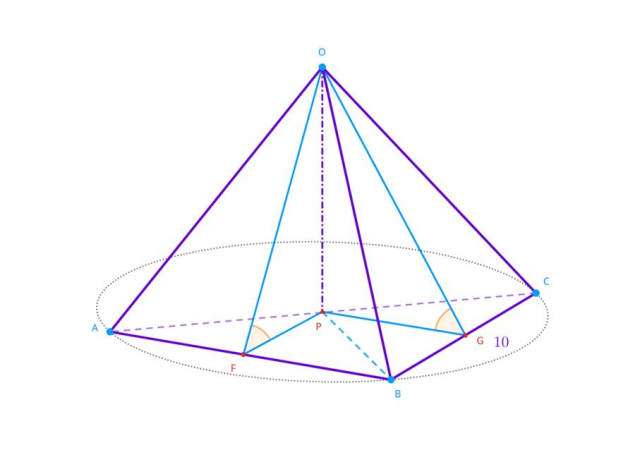
Zauważ, że spodek wysokości ostrosłupa pokrywa się ze środkiem przeciwprostokątnej podstawy.
Skorzystaj z danych wyznaczonych w poprzednim podpunkcie:
![]()
Długość odcinka CP to połowa przeciwprostokątnej trójkąta prostokątnego równoramiennego, czyli wynosi
![]() .
.
Skorzystaj z definicji funkcji trygonometrycznych w trójkącie prostokątnym:
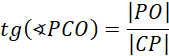
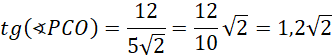
Odp. Tangens kąta nachylenia krawędzi bocznej do płaszczyzny podstawy wynosi
![]() .
.

Zauważ, że spodek wysokości ostrosłupa pokrywa się ze środkiem przeciwprostokątnej podstawy. Znając długości odpowiednich odcinków, skorzystaj z definicji funkcji trygonometrycznych w trójkącie prostokątnym i oblicz tangens kąta PCO.

Zadanie 5.1.
111Zadanie 5.2.
111Zadanie 5.4.
111Zadanie 5.5.
111Zadanie 5.6.
112Zadanie 5.7.
112Zadanie 5.8.
112Zadanie 5.37.
117Zadanie 5.39.
117Zadanie 5.41.
118Zadanie 5.42.
118Zadanie 5.43.
118Zadanie 5.46.
119Zadanie 5.49.
119Zadanie 5.50.
119Zadanie 5.51.
119Zadanie 5.54.
120Zadanie 5.60.
121Zadanie 5.62.
121Zadanie 5.63.
121Zadanie 5.64.
121Zadanie 5.65.
121Zadanie 5.67.
122Zadanie 5.69.
122Zadanie 5.70.
122Zadanie 5.71.
122Zadanie 5.72.
122Zadanie 5.73.
122Zadanie 5.74.
122Zadanie 5.75.
123Zadanie 5.76.
123Zadanie 5.77.
123Zadanie 5.78.
123Zadanie 5.79.
123Zadanie 5.80.
123Zadanie 5.81.
123Zadanie 5.82.
124Zadanie 5.83.
124Zadanie 5.84.
124Zadanie 5.85.
124Zadanie 5.86.
124Zadanie 5.87.
125Zadanie 5.88.
125Zadanie 5.91.
125Zadanie 5.92.
125Zadanie 5.93.
126Zadanie 5.95.
126Zadanie 5.96.
126Zadanie 5.97.
126Zadanie 5.98.
127Zadanie 5.110.
128Zadanie 5.112.
128Zadanie 5.121.
129Zadanie 5.126.
130Zadanie 5.133.
131Zadanie 5.134.
131Zadanie 5.136.
131Zadanie 5.141.
132Zadanie 5.144.
132Zadanie 5.145.
132Zadanie 5.148.
133Zadanie 5.155.
134Zadanie 5.156.
134Zadanie 5.157.
134Zadanie 5.158.
135Zadanie 5.159.
135Zadanie 5.160.
135Zadanie 5.170.
136Zadanie 5.172.
137Zadanie 5.185.
138Zadanie 18.
141Zadanie 19.
141Zadanie 20.
141Zadanie 21.
141Zadanie 24.
142Zadanie 25.
142Zadanie 27.
142Zadanie 29.
142Zadanie 30.
143Zadanie 32.
143
