W tym zadaniu musisz skorzystać z obwodu trzech ścian, aby wyliczyć objętość prostopadłościanu.
x – pierwsza krawędź prostopadłościanu
y – druga krawędź prostopadłościanu
z – trzecia krawędź prostopadłościanu
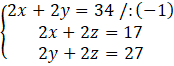
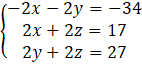
![]()
![]()
-2y + 2z + 2y + 2z = -17 + 27
4z = 10 /:4
z = 2,5
2y + 2 ∙ 2,5 = 27
2y + 5 = 27 /-5
2y = 22 /:2
y = 11
2x + 2 ∙ 2,5 = 17
2x + 5 = 17 /-5
2x = 12 /:2
x = 6
V = xyz = 6 ∙ 11 ∙ 2,5 = 165
Odp. Objętość tego prostopadłościanu wynosi 165 cm3.

Na początku musisz oznaczyć symbolami wymiary prostopadłościanu. Następnie musisz zapisać pierwsze równanie, w którym obwód pierwszej ściany (L = 2a + 2b) wynosi 34. Drugim równaniem będzie to, że obwód drugiej ściany jest równy 17. W ostatnim równaniu musisz zapisać to, że obwód trzeciej ściany jest równy 27. Na końcu musisz przemnożyć wyliczone długości krawędzi, aby uzyskać objętość tego prostopadłościanu.

Zadanie 1
84Zadanie 2
84Zadanie 4
84Zadanie 5
84Zadanie 8
85Zadanie 9
85Zadanie 10
85Zadanie 11
85Zadanie 12
85Zadanie 13
86Zadanie 14
86Zadanie 17
86Zadanie 1
87Zadanie 2
87Zadanie 3
87Zadanie 4
87Zadanie 5
87Zadanie 6
87Zadanie 7
88Zadanie 9
88Zadanie 14
89Zadanie 15
89Zadanie 16
89Zadanie 18
89Zadanie 19
89Zadanie 21
89Zadanie 1
90Zadanie 2
90Zadanie 3
90Zadanie 4
90Zadanie 5
90Zadanie 6
90Zadanie 7
90Zadanie 8
91Zadanie 9
91Zadanie 10
91Zadanie 11
91Zadanie 12
91Zadanie 13
91Zadanie 14
92Zadanie 16
92Zadanie 18
92Zadanie 21
92Zadanie 12
94Zadanie 5
97Zadanie 1
101Zadanie 6
101Zadanie 7
101Zadanie 10
102Zadanie 11
102Zadanie 12
102Zadanie 13
102
