W tym zadaniu musisz najpierw rozwiązać trzy układy równań ![]()
![]()
![]()
![]()
![]()
2x + 5 ∙ 3x = 17
2x + 15x = 17
17x = 17 /:17
x = 1
y = 3x = 3 ∙ 1 = 3
A = (1, 3)
![]()
![]()
3(19 – 4y) – 2y = 15
57 – 12y – 2y = 15 /-57
-14y = -42 /:(-14)
y = 3
x = 19 – 4y = 19 – 4 ∙ 3 = 19 – 12 = 7
B = (7, 3)
![]()
![]()
![]()
2x + 3(5x – 25) = 27
2x + 15x – 75 = 27 /+75
17x = 102 /:17
x = 6
y = 5x – 25 = 5 ∙ 6 – 25 = 30 – 25 = 5
C = (6, 5)
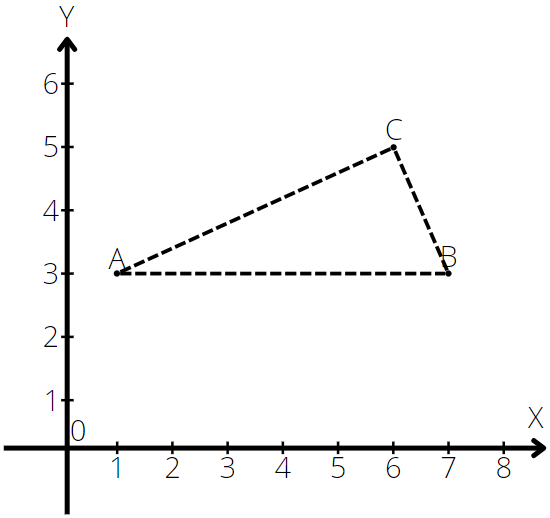
|AB| = |7 – 1| = |6| = 6
hc = |5 – 3| = |2| = 2
![]()
Odp. Pole tego trójkąta wynosi 6.

Aby rozwiązać układy równań powinieneś wyznaczyć z jednego z równań wzór na niewiadomą, a następnie podstawić ją do pozostałego równania. Po wyliczeniu wartości niewiadomej musisz podstawić ją do wyznaczonego wzoru, aby obliczyć wartość pozostałej niewiadomej. Po narysowaniu trójkąta w układzie współrzędnych musisz obliczyć długość podstawy trójkąta (musisz obliczyć wartość bezwzględną różnicy pierwszych współrzędnych wierzchołków podstawy) i wysokość (musisz obliczyć wartość bezwzględną różnicy drugiej współrzędnej pozostałego wierzchołka i dowolnego wierzchołka podstawy). Aby obliczyć pole trójkąta musisz skorzystać ze wzoru ![]()

Zadanie 1
84Zadanie 2
84Zadanie 4
84Zadanie 5
84Zadanie 8
85Zadanie 9
85Zadanie 10
85Zadanie 11
85Zadanie 12
85Zadanie 13
86Zadanie 14
86Zadanie 17
86Zadanie 1
87Zadanie 2
87Zadanie 3
87Zadanie 4
87Zadanie 5
87Zadanie 6
87Zadanie 7
88Zadanie 9
88Zadanie 14
89Zadanie 15
89Zadanie 16
89Zadanie 18
89Zadanie 19
89Zadanie 21
89Zadanie 1
90Zadanie 2
90Zadanie 3
90Zadanie 4
90Zadanie 5
90Zadanie 6
90Zadanie 7
90Zadanie 8
91Zadanie 9
91Zadanie 10
91Zadanie 11
91Zadanie 12
91Zadanie 13
91Zadanie 14
92Zadanie 16
92Zadanie 18
92Zadanie 21
92Zadanie 12
94Zadanie 5
97Zadanie 1
101Zadanie 6
101Zadanie 7
101Zadanie 10
102Zadanie 11
102Zadanie 12
102Zadanie 13
102
